Skip over navigation
Sitting Round the Party Tables
Age 5 to 11
Challenge Level 
We had some really good ideas sent in, some that were illustrated well using the computer. From Kent College we had Primrose and Charlotte, Sophie and Nia, Stephanie, Nandini and Hazel.
Well here we have a superb piece of work, sent in by Abi and Charlotte from the same school, that I would advise people to look at for working investigatively on this activity.
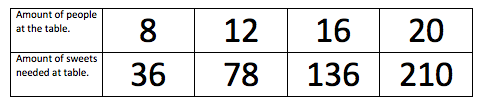
When we first looked at the problem we decided to test the
difference between the amount of sweets each table needed, and we
came up with these results.
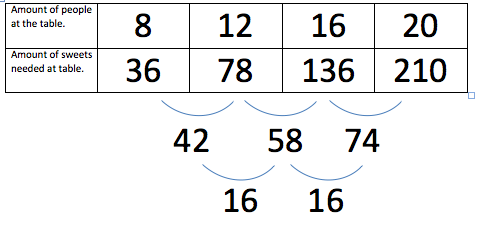
We looked at the results to see if there was a pattern in the
difference between the amounts of sweets. Despite the fact there
wasn't a pattern there we were determined to find a pattern. So we
looked further into the problem and saw a pattern between the
differences.
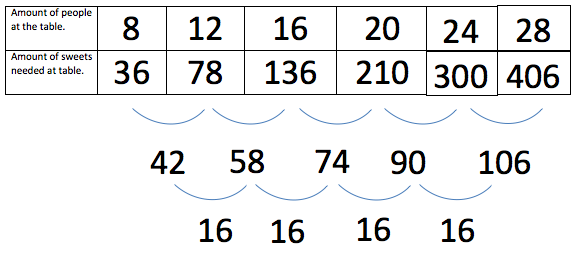
From that we could guess the next two amount of sweets
needed.
When we saw this we thought of why it could have happened.
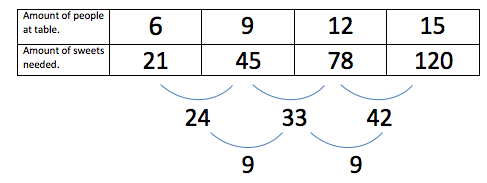
Then we realised that a square has four sides and four squared is
$16$ so to get proof we checked with a triangle.
There is a pattern. So the difference between the difference
between the difference is always nought.
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?
