Three Sets of Cubes, Two Surfaces

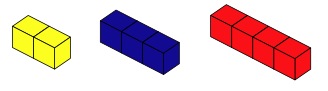
This is slightly different from Two on Five but is seen as an extension for some pupils. You might like to go there first!
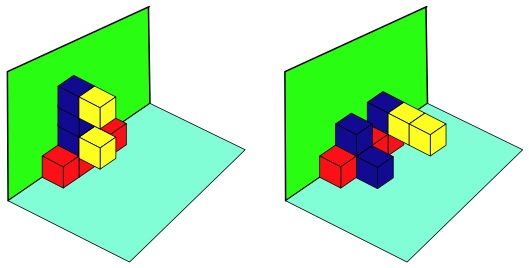
The nine cubes are to be connected in the usual way with the following rules being applied. 
The two yellow cubes are not allowed to touch the wall or floor surfaces
The Three blue cubes must touch one surface only, the wall or the floor
The four red cubes must touch both wall and floor surfaces
 
Here are two examples that obey the rules;