Skip over navigation

Inky Cube

Age 7 to 14

Challenge Level Yellow star

Primary curriculum

Here is a cube with nine small square patches on each of the six faces.

Some of the patches on each face are covered in ink.

All the faces are different.

The cube is placed on paper and makes a mark like this;

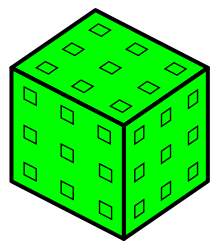
It is rolled over by tipping it very carefully (with no sliding) along one of the edges so that the next inky mark is right by its side. This gives;

It can roll both left and right and up and down.

When it has done several rolls, without taking it off, the paper looks like this;

Your challenge is to find out:

where the inky spots are on each of the six faces
where the cube was first placed
the route that the cube has taken.

All the faces might not have been used for this example.

Here is a printable version of the marks left by the cube.

--------------------

Next, you might like to try this colour version where you have to find the colours for each patch on each of the faces of the cube, as well as the route it took.

Here is a printable version of the marks left by this coloured cube.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Inky Cube

You may also like

Plants

Junior Frogs

Three Sets of Cubes, Two Surfaces