Skip over navigation
Amir sent us this solution:

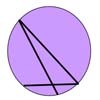
Draw any chord passing through $P$, and call its endpoints $Q$ and $R$. Let $a$ be the length of the line segment $PQ$, and $b$ the length of $PR$.
If $a=b$, then clearly $P$ is the midpoint of a chord, so we're done. So suppose that $a\neq b$. We may as well assume that $a< b$ (otherwise just switch round $Q$ and $R$). Imagine that the shape is made out of a metal frame, and that the chord $QR$ is made from elastic, just looped round the frame at $Q$ and at $R$, but fixed at $P$ (so that it can rotate). Rotate the chord around $P$, and the elastic will stretch so that the line is always a chord of the shape. When it's gone 180$^{\circ}$ round, $QP$ will have length $b$, and $PR$ will have length $a$, in other words, the segments will have switched. So now $|QP|> |PR|$, when they started the other way round. But as we turn the chord, the lengths of the segments change continuously, so to switch from $QP$ being shorter to $QP$ being longer, we must have had $|QP|=|QR|$ at some point. But then $P$ will be the midpoint of this chord.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Middle Man
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Amir sent us this solution:

Draw any chord passing through $P$, and call its endpoints $Q$ and $R$. Let $a$ be the length of the line segment $PQ$, and $b$ the length of $PR$.
If $a=b$, then clearly $P$ is the midpoint of a chord, so we're done. So suppose that $a\neq b$. We may as well assume that $a< b$ (otherwise just switch round $Q$ and $R$). Imagine that the shape is made out of a metal frame, and that the chord $QR$ is made from elastic, just looped round the frame at $Q$ and at $R$, but fixed at $P$ (so that it can rotate). Rotate the chord around $P$, and the elastic will stretch so that the line is always a chord of the shape. When it's gone 180$^{\circ}$ round, $QP$ will have length $b$, and $PR$ will have length $a$, in other words, the segments will have switched. So now $|QP|> |PR|$, when they started the other way round. But as we turn the chord, the lengths of the segments change continuously, so to switch from $QP$ being shorter to $QP$ being longer, we must have had $|QP|=|QR|$ at some point. But then $P$ will be the midpoint of this chord.
You may also like
Fixing It
A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?
OK! Now Prove It
Make a conjecture about the sum of the squares of the odd positive integers. Can you prove it?

