Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Population Dynamics - Part 5
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem ?
Practice with the use of numbers is a crucial biological skill. These interesting questions will allow you to practise these skills whilst developing awareness of orders of magnitude in scientific contexts.Possible approach
There are several parts to this question. The individual pieces could be used as starters or filler activities for students who finish classwork early. Enthusiastic students might work through them in their own time. Since there is no absolutely 'correct' answer to many of these questions, they might productively be used for discussion: students create their own answers and then explain them to the rest of the class. Does the class agree? Disagree? Is there an obvious best 'collective' answer?Key questions
- What assumptions will you need to make in this question?
- How accurate do you think you answer is?
- What order of magnitude checks could you make to test that your answer is sensible?
Possible extension
Can students make up similar questions? Can they put any upper or lower bounds on the numbers?Possible support
Students might struggle with the 'open' nature of the questions. To begin, they might like to read the Student Guide to Getting Started with rich tasksRelated Collections
You may also like
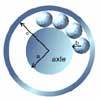
Ball Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built without mortar on a flat horizontal surface, to overhang by 1 metre? How big an overhang is it possible to make like this?
Cushion Ball
The shortest path between any two points on a snooker table is the straight line between them but what if the ball must bounce off one wall, or 2 walls, or 3 walls?

