Skip over navigation
A computer is programmed to produce a long string of Hs and Ts which are printed out onto a piece of ticker tape which has been divided into square boxes.
Each time a button is pressed the tape advances by one 'unit' and the bottom box cut off, so there are always three boxes visible in a line. The number of units of paper remaining inside the machine is indicated in the circle.
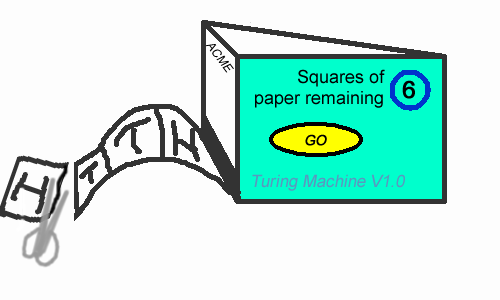
Alan Turing, the great code breaker, and I are each given a slip which we each mark with Hs and Ts. Whoever sees their sequence emerge first from the machine wins. I choose HTT and Turing chooses HHT as shown in the diagram.
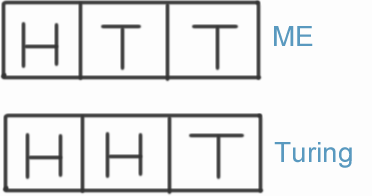
If the machine configuration is as shown in the diagram at the moment, who is more likely to win: Turing or me?
Suppose we were going to play again and Turing chooses the sequence THT. Being a bit of a spy, I find this information out before I choose my sequence. Before we play we are going to reload the machine so that it contains 6 units of paper. Can I choose a sequence which is more likely to win than Turing's?
Difficult Extension: After playing with these choices many times, Turing is fed up with losing and wants to choose TTH. He also wants to load the machine with infinitely many units of paper. Can I choose a sequence which is more likely to beat Turing's new choice?
Ante Up
Age 16 to 18
Challenge Level 
A computer is programmed to produce a long string of Hs and Ts which are printed out onto a piece of ticker tape which has been divided into square boxes.
Each time a button is pressed the tape advances by one 'unit' and the bottom box cut off, so there are always three boxes visible in a line. The number of units of paper remaining inside the machine is indicated in the circle.
Alan Turing, the great code breaker, and I are each given a slip which we each mark with Hs and Ts. Whoever sees their sequence emerge first from the machine wins. I choose HTT and Turing chooses HHT as shown in the diagram.
If the machine configuration is as shown in the diagram at the moment, who is more likely to win: Turing or me?
Suppose we were going to play again and Turing chooses the sequence THT. Being a bit of a spy, I find this information out before I choose my sequence. Before we play we are going to reload the machine so that it contains 6 units of paper. Can I choose a sequence which is more likely to win than Turing's?
Difficult Extension: After playing with these choices many times, Turing is fed up with losing and wants to choose TTH. He also wants to load the machine with infinitely many units of paper. Can I choose a sequence which is more likely to beat Turing's new choice?
You may also like
Rain or Shine
Predict future weather using the probability that tomorrow is wet given today is wet and the probability that tomorrow is wet given that today is dry.
Squash
If the score is 8-8 do I have more chance of winning if the winner is the first to reach 9 points or the first to reach 10 points?
Playing Squash
Playing squash involves lots of mathematics. This article explores the mathematics of a squash match and how a knowledge of probability could influence the choices you make.