Skip over navigation
As the disc makes a single lap of the tray, what parts of the tray will have made contact with the disc? How far is this?
Read the article A Rolling Disc - Periodic Motion.
Five Circuits, Seven Spins
Age 16 to 18
Challenge Level 
Why do this problem?
This is a good problem for discussion and developing clear visualisation and mathematical communication. It relates the angle of rotation of a circle to a distance and is therefore of use in exploring radians and the formula $s=r\theta$.Possible approach
Students' abilities to visualise the meaning of this problem might vary considerably. As such, this problem can appear to be difficult until a clear approach to the solution is found. The behaviour of the disc at the corners is likely to cause the most difficulty in imagining the rotation. As a result, students might need to be given a variety of visual devices to allow them to get started. For example:- Imagine looking down onto the tray and watching the disc rotate about its centre.
- Imagine breaking the journey into a series of straight line trips.
- Imagine that the disc is pinned down in the centre and the tray is a track moved around the disc.
- Imagine that the edge of the disc is coated in ink. Which parts of the tray would be coloured following a lap of the track?
- Roll a coin around a book and use the head on the coin as a reference. Does the head rotate as it moves through a corner (i.e. when moving from a horizontal to a vertical part of the the journey).
This is the sort of problem which becomes much clearer once a
solution has been found. Once students have solved the problem they
should try to rewrite their answer and method as clearly as
possible, in a way which is both simple but complete.
It is possible to tackle this problem using degrees and the
formula for the circumference of a circle, but it is much simpler
to solve using radians and the formula $s=r\theta$.
Key questions
How far does the centre of a disc move in one revolution when
the plate is in contact with a straight edge?
What mathematics allows us to relate this distance to an
angle?
What units should we measure the angle of rotation in?
Why?
If the disc has rotated $7$ full times, how far must it have
rolled?
As the disc makes a single lap of the tray, what parts of the tray will have made contact with the disc? How far is this?
Possible support
Consider the distance a bicycle travels when the wheels rotate once.Read the article A Rolling Disc - Periodic Motion.
Possible extension
Try the problem ContactYou may also like
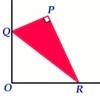
Set Square
A triangle PQR, right angled at P, slides on a horizontal floor with Q and R in contact with perpendicular walls. What is the locus of P?
Mach Attack
Have you got the Mach knack? Discover the mathematics behind exceeding the sound barrier.
Construct the Solar System
Make an accurate diagram of the solar system and explore the concept of a grand conjunction.