Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Angle of Shot



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
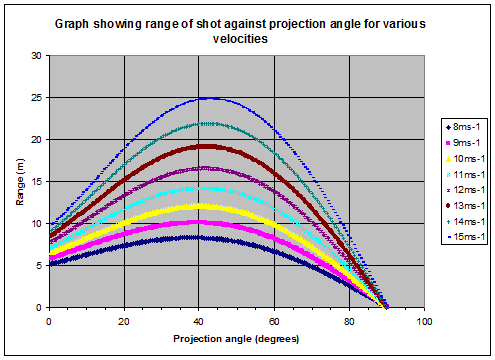
Assuming for the time being that the athlete can launch the shot at the same speed at any angle, I plotted a graph of range against projection angle for a variety of speeds:
Looking at the graph, it appears the optimal angle for maximising range is slightly smaller than $45^{\circ}$.
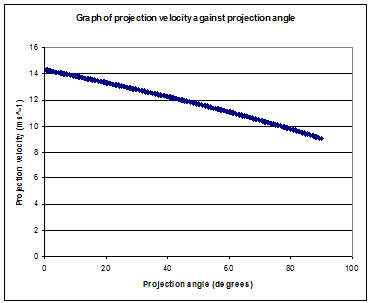
We now need to incorporate how the maximum launch speed varies with the projection angle. Here's a graph of projection velocity against projection angle. Although the projection velocity decreases as the projection angle increases, the range previously had a maximum at $45^{\circ}$, so the optimal angle will now be a tradeoff between angle and velocity.
We can now calculate the range of the shot using this projection velocity, and plot a graph of range against projection angle (using the same value of the parameters as before):
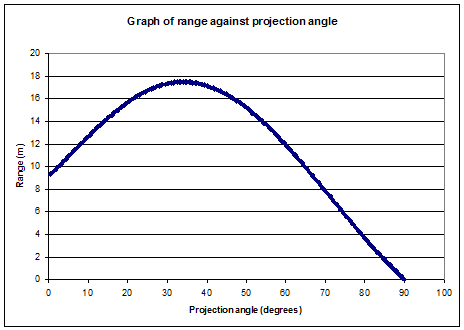
For these values of the parameters,we can see the optimal angle is now around $35^{\circ}$, as opposed to $45^{\circ}$ in the previous model.
Solving this problem using differentiation is quite messy, but well done to Joshua who had a go; you can see what he did here.
You may also like
Whoosh
A ball whooshes down a slide and hits another ball which flies off the slide horizontally as a projectile. How far does it go?
Escape from Planet Earth
How fast would you have to throw a ball upwards so that it would never land?