Fit for Photocopying

Why do this problem?

Most students will be familiar with the $A$ paper sizes but they may be unaware of their special properties. This problem explores ratio and scaling, with the possibility of working with surds and indices if students choose to tackle the extension questions.

Possible approach

Take a sheet of $A4$ paper, hold it up to show the class.
"Here is a sheet of $A4$ paper." 

Fold it in half so that it is $A5$ size.
"Does anyone know what size this paper is?"
"$A5$"
"What special relationships can you think of between $A4$ and $A5$ paper?"
 "The area is half"
"The long side on the $A5$ is the same as the short side on the $A4$"
"They are similar shapes"
 
If similarity doesn't emerge as a suggestion from the class, use the example of a photocopier - something printed on $A4$ paper can be enlarged to fit onto $A3$ without distortion, so they must be similar rectangles.

Set the students the challenge of working out the ratio of the shorter to the longer side of a sheet of A paper. This diagram may be useful:
   
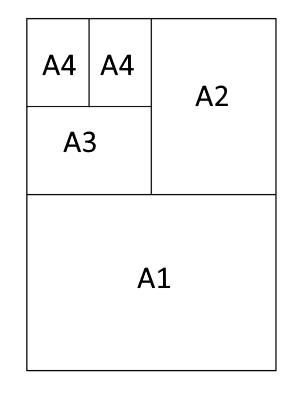
If students are having difficulty knowing where to start, suggest that they label the two shortest lengths in the diagram $x$ and $y$, and then work out the other lengths.

Once they have established that the sides are in the ratio $1:\sqrt2$, reveal that a sheet of A0 paper has an area of one square meter, and invite them to calculate the dimensions of the different paper in the A family. 

Possible support

Growing Rectangles explores length and area scale factors and might be appropriate for some students to work on before attempting this task.

Possible extension

Invite students to come up with a consistent definition for fractional or negative paper sizes.