Big and Small Numbers in Chemistry

• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science

Chemistry makes good use of numbers both small and large. Try these questions involving big and small numbers. You might need to use standard physical data not given in the questions. The questions all involve some aspect of approximation, although you might be able to give rather accurate upper and lower bounds on the actual quantities in some cases. In all cases it is good to be clear in your own mind as to the precision of the answers given, and use an appropriate level of rounding in each case.

 
1) How many copper atoms are there in a one pence piece? How many electrons are there?
 
2) What volume of air would you have to contain to have enough argon to fill a lightbulb?
 
3) If you cooled all of the air from part 2 until none of the matter was in gaseous form, what volume would it occupy at standard pressure?
 
4) A Teflon monomer looks like this:

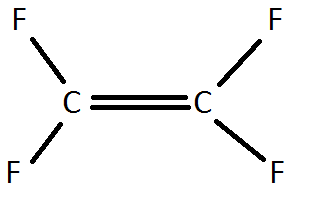
Draw a Teflon polymer. What percentage, by mass, of Teflon is carbon?
 
5) If the C-C bond length in Teflon is about 140pm (1pm = $10^{-12}m$), how many fluorine atoms would there be in a polymer measuring 1cm in length? How many moles of $F_{2}$ gas would contain the same number of fluorine atoms?
 
6) Alkali metals (group 1) react with water to produce MOH (M is the symbol used for an unknown metal) .Write a reaction for this. What gas is produced? What volume of water would you have to use in this reaction to produce 1.5 moles of gas?
 
7) A hydrogen atom has a radius of 120pm . Its nucleus has a radius of 1.75fm (1fm = $10^{-15}m$). What is the rest of the atom made up of? Estimate the percentage of the volume of a hydrogen atom that is empty space.
 
8) 25.5% of the atoms in your body are oxygen. This is equivalent to 65% of your body weight! If 9.5% of the atoms in your body are carbon, what percentage of your body weight is this? Estimate how many atoms there are in your body in total.
 
9) Looking at questions 7 and 8, if all of the atoms in your body were placed end-to-end, how long would the line be? Can you think of (or find out about) something that is that far away from you now?