Skip over navigation

Sports Equipment

Age 7 to 11

Challenge Level Yellow star

Sports Equipment

I've collected together these different balls that are used in various sports:

as well as some others!

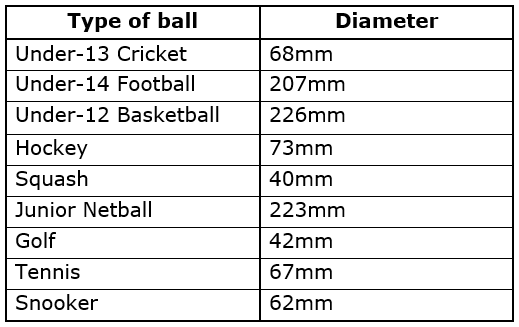
Here are the standard diameters of the different types of ball:

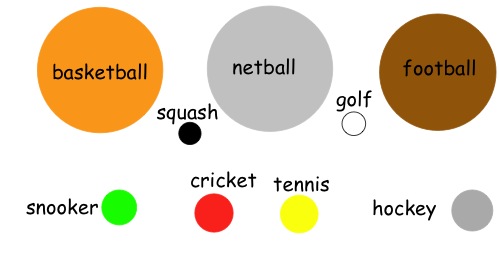
Here is a scale drawing of the balls:

You might like to find a few different balls at school to get a feel for their different sizes before trying this challenge.

Try using the diameter information to make circles the right size and use them to explore.

If a line is drawn on the ground and the balls are put on that line with each ball touching the one in front and the one behind, which arrangement makes the shortest line of balls?

Which arrangement makes the longest line of balls?

Why do this problem?

This activity offers the opportunity for pupils to think in creative ways as they explore the relationships between differently-sized balls. Through the physical manipulation of the circles, which represent the balls, learners will come to a better understanding of circle properties.

Possible approach

Introducing this task using the school's own stock of sports equipment is likely to grab children's attention. Show the class all the different balls you have gathered together and invite them to talk about what they notice. They are likely to suggest all sorts of things, perhaps related to the sport that each is used for, or the material each is made of, in addition to their spherical shape (or approximate spherical shape).

Introduce the challenge and give pairs of children time to work on it. Allow them to decide how to approach the task and give them free choice of equipment and resources. Some pairs may want to experiment with the balls themselves, some may want to know the diameters so they can make representations, others may have completely different ways of having a go at the challenge.

It would be worthwhile to stop everyone after a suitable length of time so that learners can share where they have got to so far. You could warn two or three pairs that you'd like them to talk about how they are going about the task. This discussion may well inspire some pairs to change their methods, but do allow them to make that decision themselves. This is also a chance to clarify the 'rules' of the activity. Pairs may need reminding that each ball must touch both the one in front and the one behind it. Placing very small balls in between two large ones may not satisfy this condition!

This activity could be presented as a 'simmering' task, meaning that it is worked on over an extended period of time. Children could post up their longest or shortest lines on a designated wall area so that the challenge becomes to better the best so far. You can then allocate a time to reflect on the class' results and invite them to justify their findings. Are they sure this is the longest/shortest line? How do they know?

Key questions

What have you decided to do?

Tell me what you have here.

Would you change anything here?

Could you make the line longer/shorter?

How do you know you have made the longest/shortest line?

Possible extension

Pupils who easily manage the activity could be further challenged by asking them to place the equipment in lines that make up an equilateral triangle or a square.

Possible support

Some pupils may be able to do the activity without the balls but not have the ability to produce the circles accurately without adult support. You could give some pairs copies of this sheet with the circles already drawn.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Sports Equipment

Sports Equipment

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

Shaping It