Cylinder Cutting

 We start off with this tube (like one from inside a roll of kitchen paper):

 

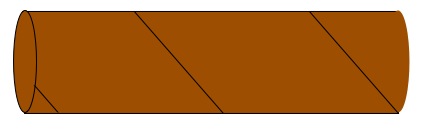
The tube has a seam running through it (that forms a helix) .You'll have to carefully cut along that seam and then open it out and flatten it a little.
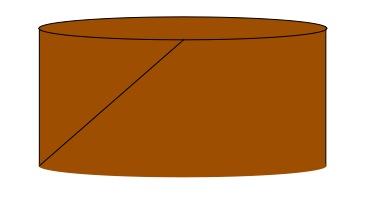
Now you will notice a parallelogram. It will very easily return to the original cylinder shape, BUT we can produce another cylinder by putting the two shorter edges together. 
Then you have a cylinder that looks more like this:

 

You are now encouraged to consider taking an $A4$ sheet of paper and cutting it at an angle, in such a way that you can roll it up to produce a similar cylinder (like the kitchen roll one). You then repeat the same cutting as above and create the second cylinder by rolling it up differently.
 
Examine the lengths and volumes of these two cylinders and the areas of the paper pieces.
 
Try many different examples by cutting differently.
 
Is there a way of cutting the $A4$ sheet to produce a shape in which both cylinders have the same volume?

Explore further the shaped pieces you've produced.