Changing Areas, Changing Perimeters

Why do this problem?

Working on this problem will give students a deeper understanding of area and perimeter, and how they change as a shape is altered. The problem will address some students' misconception that as area increases, perimeter must necessarily increase too. 

Possible approach

Display a simple shape made out of squares on a small square grid:

 

 

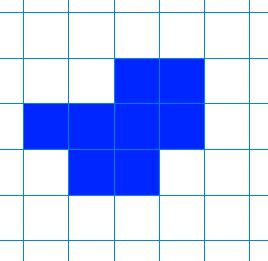
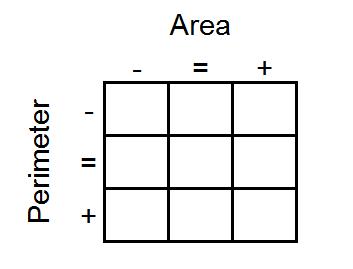
As each pair finishes, they can be given the second set of cards to work on in the same way. For those who finish quickly, ask them the question from the problem about extending the grid like this:
 

Towards the end of the lesson, bring the class together to share any efficient ways they found to compare areas and perimeters without having to work them all out.
 
In sharing feedback on the first activity, ask students what they notice about the shapes on the top row of the grid. 

To explain why all shapes drawn by cutting corners out of a 4 by 4 square have a perimeter of 16, these images might be useful:
 
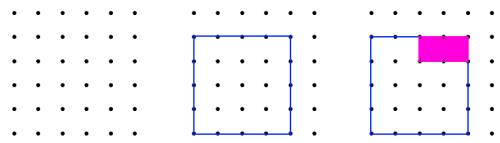
"How much perimeter has been lost by cutting out the pink rectangle? How much has been gained?"
Shapes on the second and third row can be compared in the same way.

For the second activity, we want students to recognise:
"Rectangles that are closer to squares have smaller perimeters than long thin rectangles with the same area"

One prompt that could draw out this thinking might be:
"If two rectangles have the same area but different perimeters, how can I decide which has the greater perimeter?"
 
Finally, discuss the possible content of the four extra spaces in the extended grid, focussing in particular on why some of the spaces are impossible to fill in.

Possible support

Area and Perimeter provides a good starting point for the thinking expected of students in this problem. 
 

Possible extension

Finally, students could be challenged to create their own set of cards with a $1$ by $5$ rectangle as the central card. This forces them to consider rectangles whose side lengths are not whole numbers.