Changing Areas, Changing Perimeters
Isabelle from South Wilts and Natalie from St.Andrews International School in Thailand both answered the first challenge correctly.
Here is Natalie's arrangement of the shapes:
Here is how Isabelle described her strategy:
a) Write down the areas and perimeters of each shape.
b) The only three shapes that share an area are G, A & C therefore they must occupy the middle column.
c) B, D & I have areas less than 14 so must occupy the left column and E, F & H have areas greater than 14 so must occupy the right column.
d) The shapes with perimeter 20 (B, C & H) must go in the bottom row, those with perimeter 18 must go in the middle row and those with perimeter 16 must go in the top row.
There is only one way this can be achieved so by a process of elimination the solution is as above.
Isabelle also answered the second challenge correctly:
| AREA | ||||
|---|---|---|---|---|
| - | = | + | ||
| - | 2 by 7 | 4 by 4 | 3 by 6 | |
| PERIMETER | = | 1 by 9 | 2 by 8 | 5 by 5 |
| + | 1 by 15 | 1 by 16 |
3 by 8
|
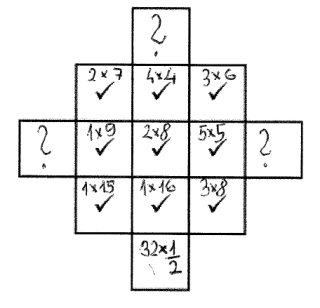
It's possible to fill in the box on the left too. I wonder if you can think of a way, and convince yourself that it's impossible to fill in the top and right boxes.
You may also like
Framed
Seven small rectangular pictures have one inch wide frames. The frames are removed and the pictures are fitted together like a jigsaw to make a rectangle of length 12 inches. Find the dimensions of the pictures.
Tilted Squares
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
Four or Five
The diagram shows a large rectangle composed of 9 smaller rectangles. If each of these rectangles has integer sides, what could the area of the large rectangle be?