Filling the Gaps

Age 14 to 16

Challenge Level Yellow star

Charlie has been thinking about which numbers can be written as a sum of two square numbers. He took a $10\times10$ grid, and shaded the square numbers in blue and the sums of two squares in yellow.

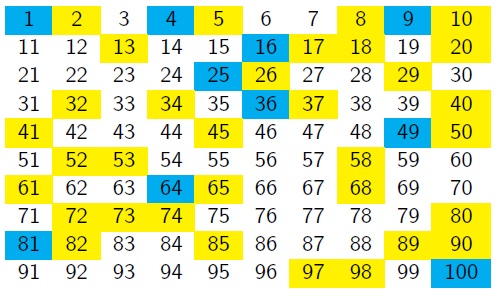
He hoped to find a pattern, but couldn't see anything obvious.
Vicky suggested changing the number of columns in the grid, so they reduced it by one:

"There seems to be a diagonal pattern."

"If the rows were one shorter, then those diagonals would line up into vertical columns, wouldn't they?"

"Let's try it..."

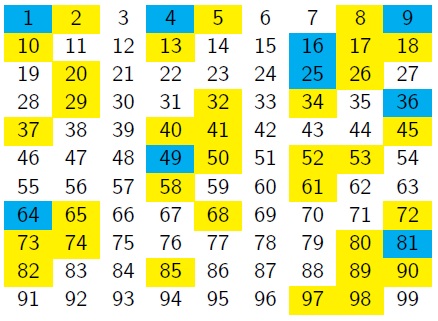
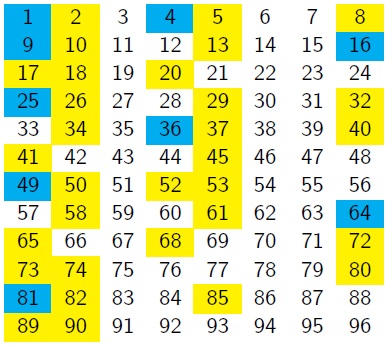
What do you notice about the positions of the square numbers?
What do you notice about the positions of the sums of two square numbers?

Can you make any conjectures about the columns in which squares, and sums of two squares, would appear if the grid continued beyond 96?

Can you prove any of your conjectures?

You might like to look back at the nine-column grid and ask yourself the same questions.

Charlie couldn't write every number as a sum of two squares. He wondered what would happen if he allowed himself three squares.

Will any of the numbers in the seventh column be a sum of three squares?

Can you prove it?

"We must be able to write every number if we are allowed to include sums of four squares!"

"Yes, but it's not easy to prove. Several great mathematicians worked on it over a long period before Lagrange gave the first proof in 1770."

With thanks to Vicky Neale who created this task in collaboration with NRICH.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Filling the Gaps

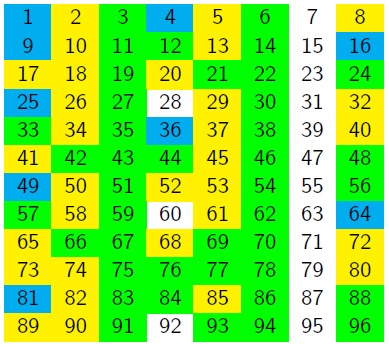
You may also like

More Mods

Mod 3

Novemberish