Building with Rods

Age 7 to 11

Challenge Level Yellow star

Building with Rods

We have three rods that are each 2 units long.

The different colours are used to make the diagrams clearer and they always remain in the same place i.e the blue as the bottom layer, the green as the top layer and the red as the middle layer.

The challenge is to find how many different ways you can stack these rods.

The rule is that one or both of the small cubes must sit squarely on top of other small cubes.

It does not matter if they are likely to topple over.

Both these two arrangements fit the rule.

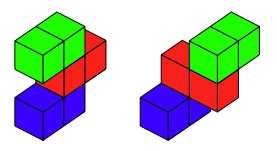
However, these two arrangements do not fit the rule as the rods have to be lined up squarely and each little cube must sit on top of one other cube and not overlap two cubes.

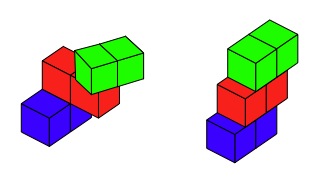
How can you convince someone that you have found all the possibilities?

Why do this problem?

This activity acts as a further extension to Two on Five. It's an activity that is intended for curious pupils to give them opportunities to explore a spatial context using their intuition and flair. It also provides an opportunity to create a system for solving such problems. The "Teacher Support" at the bottom of this page is recommended in regard to the curiosity aspect of this task.

Possible approach

As this activity is intended to challenge the 'best' problem solvers in the class, it might be presented as on the website or in a one-to-one situation, encouraging discussion between adult and pupil. The pupils may need access to a computer program for drawing solutions.

Key questions

Tell me about what you have found.
Can you describe the ways that you arrived at these shape arrangements?
How did you construct these on the computer?

Possible extension

For those who are successful, they should be encouraged to try Building with Longer Rods.

Possible support

It will probably be helpful to have interlocking cubes available and different kinds of squared paper.

Teacher Support

This task was created to help in the pursuance of curiosity within the Mathematics lessons.
Help may be found in the realm of curiosity in watching parts of these excellent videos.
Firstly "The Rise & Fall of Curiosity", particularly the extract [23.50 - 37.15] on "adult encouragement answering and teacher behaviour."
Secondly, "The Hungry Mind: The Origins of Curiosity", particularly the extract [8.22 - 12.29] on "Children asking questions"

First can also be found at - https://www.youtube.com/watch?v=X-0NOrIU67w
Second can also be found at https://www.youtube.com/watch?v=Wh4WAdw-oq8

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Building with Rods