Skip over navigation
Building with Rods
Age 7 to 11
Challenge Level 
We had a number of really good solutions sent in from Caledon East Public School in Canada. Different answers have been obtained because of deciding what is and is not allowed.
First of all Edwin's:
The blue brick has 2 possible positions: Flat and upright. For flat, there are 9 possibilities for the red brick. For upright, there are 5 possibilities for the red brick.
The red brick stands upright in this 3 times (twice on the flat blue and once on the upright). When the red brick stands upright, there are 5 possibilities for the green brick. When the red brick is flat (and there are 11 possible positions for the red brick when it is flat), there are 9 possibilities for the green brick.
How I could convince someone that I had found all the possibilities:
I could convince someone that I had found all the possible ways to stack these blocks either by explaining my equation or by getting out some blocks to show them that I am correct.
Edwin has been creative in thinking of the vertical arrangements.
Then Guangyan wrote:
Ӭ
I think the answer is infinity. If my theory is true, that a shape's orientation is a different shape because that if you mark each corner, it would be different. So the bottom cubes could be put virtually anywhere, and that is why I think the answer is infinity.
Another creative thought from Guangyan that shapes can be put in an infinite number of different places.
Adrian sent in a part of a spreadsheet:
Ӭ
My answer is 232 and my work is messy so you may not be able to understand my work. This area in the Excel Sheet is my work for this question:
Opkar and Navin wrote that they found 125 combinations using a formula after drawing a few
combinations to see the pattern.
Dylan sent in his work:
Ӭ
This is our solution. Our final finished answer is 271, we came up with this solution by trying to find formulas and adding any other types of combinations that were not in our formula. We apologize for any mistakes and messy work/typos.
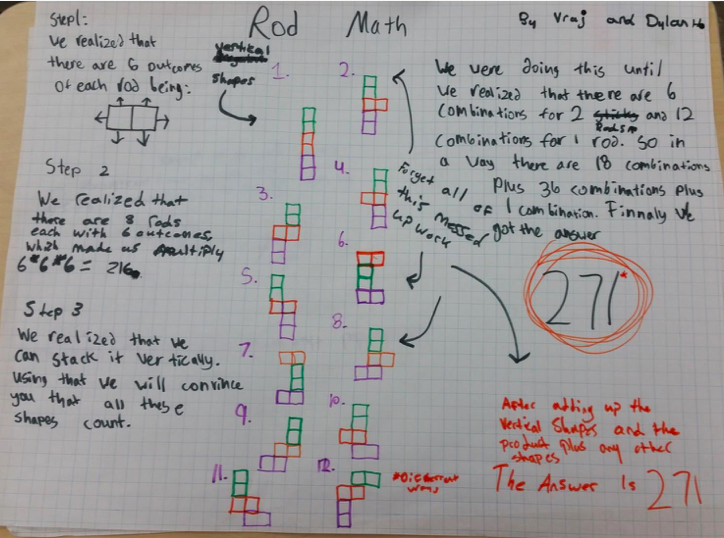
I've included this work because it shows a good start but there is a little more to do.
Waliyya wrote:
I think the answer is 162 because I know that the bottom rod has 2 possibilities, vertical and horizontal and the two rods on top had 9 possibilities (Horizontal, vertical, hanging out, forward, backward, and all of those except for horizontal on the other side) which is why I did 2 x 9 x 9 which was 162.
Finally Nikhitha also went for 162:
I believe the answer to this problem is 162. I believe this because the rod on the bottom has two positions which are vertical and horizontal and the middle and top rod have nine movements each so the calculation I did was 9 x 9 x 2 which gave me my answer 162.
Waliyya and Nikhitha worked with their own criteria about what was possible and therefore they came to make the total number 192.
Oskar and Brandan from Stanley Park Junior School, Carshalton sent in this:
There are 49 possible combinations of cuboids, because there are 7 possible ways of stacking 1 cuboid aloft another. Because of this there are 7 possibilities for red and blue and for each of these cases there are 7 more possibilities of combinations so there are 7 x 7 or 49 total sculptures.
Thank you Oskar and Brandan for your work - you stuck to horizontal arrangements and got therefore 49 as the answer.
Thank you everyone. If you are looking at this as a new activity you may find different answers according to the 'rules' you agree on.
First of all Edwin's:
The blue brick has 2 possible positions: Flat and upright. For flat, there are 9 possibilities for the red brick. For upright, there are 5 possibilities for the red brick.
The red brick stands upright in this 3 times (twice on the flat blue and once on the upright). When the red brick stands upright, there are 5 possibilities for the green brick. When the red brick is flat (and there are 11 possible positions for the red brick when it is flat), there are 9 possibilities for the green brick.
How I could convince someone that I had found all the possibilities:
I could convince someone that I had found all the possible ways to stack these blocks either by explaining my equation or by getting out some blocks to show them that I am correct.
Edwin has been creative in thinking of the vertical arrangements.
Then Guangyan wrote:
Ӭ
I think the answer is infinity. If my theory is true, that a shape's orientation is a different shape because that if you mark each corner, it would be different. So the bottom cubes could be put virtually anywhere, and that is why I think the answer is infinity.
Another creative thought from Guangyan that shapes can be put in an infinite number of different places.
Adrian sent in a part of a spreadsheet:
Ӭ
My answer is 232 and my work is messy so you may not be able to understand my work. This area in the Excel Sheet is my work for this question:
Opkar and Navin wrote that they found 125 combinations using a formula after drawing a few
combinations to see the pattern.
Dylan sent in his work:
Ӭ
This is our solution. Our final finished answer is 271, we came up with this solution by trying to find formulas and adding any other types of combinations that were not in our formula. We apologize for any mistakes and messy work/typos.
I've included this work because it shows a good start but there is a little more to do.
Waliyya wrote:
I think the answer is 162 because I know that the bottom rod has 2 possibilities, vertical and horizontal and the two rods on top had 9 possibilities (Horizontal, vertical, hanging out, forward, backward, and all of those except for horizontal on the other side) which is why I did 2 x 9 x 9 which was 162.
Finally Nikhitha also went for 162:
I believe the answer to this problem is 162. I believe this because the rod on the bottom has two positions which are vertical and horizontal and the middle and top rod have nine movements each so the calculation I did was 9 x 9 x 2 which gave me my answer 162.
Waliyya and Nikhitha worked with their own criteria about what was possible and therefore they came to make the total number 192.
Oskar and Brandan from Stanley Park Junior School, Carshalton sent in this:
There are 49 possible combinations of cuboids, because there are 7 possible ways of stacking 1 cuboid aloft another. Because of this there are 7 possibilities for red and blue and for each of these cases there are 7 more possibilities of combinations so there are 7 x 7 or 49 total sculptures.
Thank you Oskar and Brandan for your work - you stuck to horizontal arrangements and got therefore 49 as the answer.
Thank you everyone. If you are looking at this as a new activity you may find different answers according to the 'rules' you agree on.
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
