pdf Stories

Consider the following curves, with scales chosen so as to make their integrals between the endpoints equal to 1. Curves with a finite domain are indicated with a vertical line, and the axes are assumed to intersect at the origin. Make up some statistical situations, either from mathematics or from science, which would plausibly result in one of these curves as a probability density function.

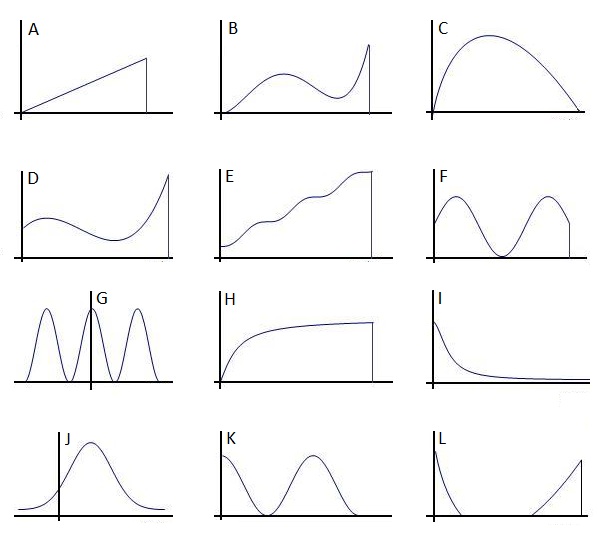
Keep your eyes open for curves in other areas of mathematics.Would they be potential candidates (ignoring scale) for probability density functions? What mathematical descriptions might accompany them? What scientific situations might they describe?

Pure maths extension: Find algebraic expressions for curves such as these, with parameters and domain chosen so as to make their integrals equal to 1 (exactly or approximately, as approriate)