Skip over navigation
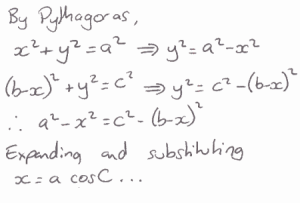

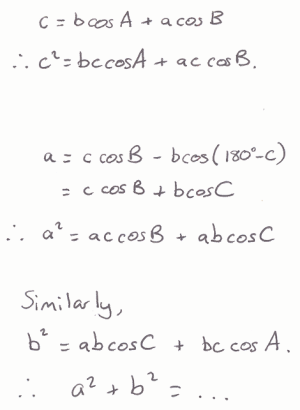
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Calculating with Cosines
Age 14 to 18
Challenge Level 





If you are a teacher, click here for a version of the problem suitable for classroom use, together with supporting materials. Otherwise, read on...
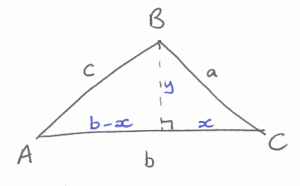
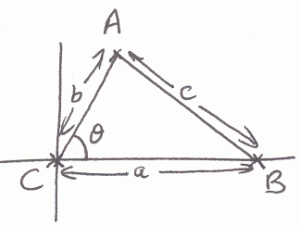
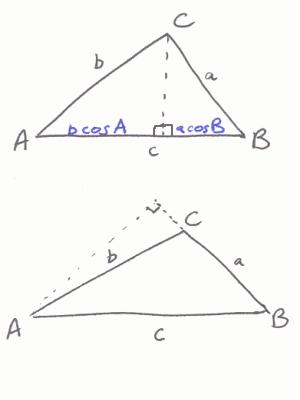
If I tell you two sides of a right-angled triangle, you can easily work out the third using Pythagoras' theorem. But what if the angle between the two sides is not a right angle? Is there a way to work out the length of the third side?
Some students tried to work out a formula to work out the length of the third side when we know two sides and the angle between them.
Below, you can see the start of their methods. Can you finish each method to produce a formula?
Student 1:

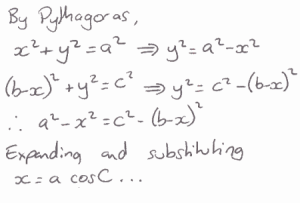
Student 2:


Student 3:

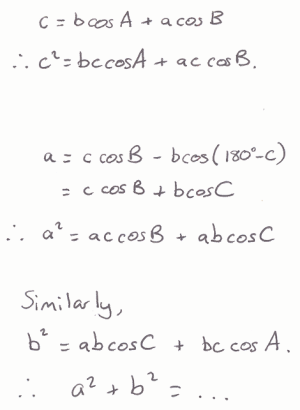
Does each method lead to an equivalent formula?
Does each method work for both acute-angled and obtuse-angled triangles?

