Skip over navigation
Tetra Square
Age 14 to 18
Challenge Level 
This problem has been replaced by Tetra Slice
ABCD is a regular tetrahedron and the points P, Q, R and S are the midpoints of the edges AB, BD, CD and CA. Prove that PQRS is a square.
You may also like
Circles Ad Infinitum
A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
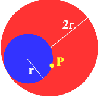
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...