Steps to the Podium

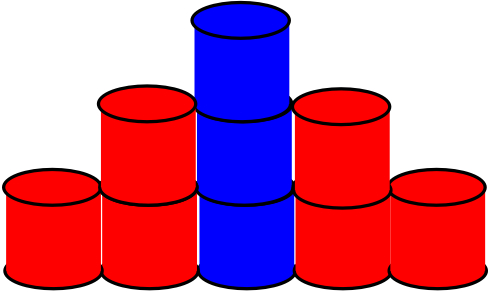
There is a raised step, often called a podium (see blue above), which you can get to by the two sets of steps, one on either side (red).

The steps and the podium are made out of cylinder blocks, each block the same size.

The picture above shows a $2$ step set of steps on either side of the podium and the total number of blocks is $9$.

The podium is always just one block higher than the top step. So you can explore the number of blocks that are necessary if the podium is $4$, $5$, $6$ . . . etc. blocks high and there is the required number of steps on either side.

Now that's not difficult. But now, suppose that there are three sets of steps, rather than two, leading up to the podium, or four, five six . . . etc. What about the number of blocks that are needed for the increasing height of the podium?

When you've got all the results of the number of blocks required no matter what the situation is, you will have a large set of numbers.

Explore these numbers.

Can you generalise? Maybe find a way of knowing very quickly how many blocks are needed for a certain number of steps up to the podium given the number of sets of steps around the podium?

Can you find other things to explore with the sets of numbers that you have now?