Steps to the Podium

Age 7 to 14

Challenge Level Yellow star

Steps to the Podium

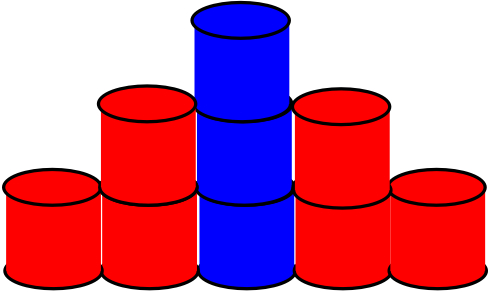
There is a raised step, often called a podium (see blue above), which you can get to by the two sets of steps, one on either side (red).

The steps and the podium are made out of cylinder blocks, each block the same size.

The picture above shows a $2$ step set of steps on either side of the podium and the total number of blocks is $9$.

The podium is always just one block higher than the top step. So you can explore the number of blocks that are necessary if the podium is $4$, $5$, $6$ . . . etc. blocks high and there are the required number of steps on either side.

Now that's not difficult. But now, suppose that there are three sets of steps, rather than two, leading up to the podium, or four, five six . . . etc. What about the number of blocks that are needed for the increasing height of the podium?

When you've got all the results of the number of blocks required no matter what the situation is you will have a large set of numbers.

Explore these numbers.

Can you generalise? Maybe find a way of knowing very quickly how many blocks are needed for a certain number of steps up to the podium given the number of sets of steps around the podium?

Can you find other things to explore with the sets of numbers that you have now?

Why do this problem?

This activity is specially designed for the highest-attaining pupils that you ever come across. So it is seen as an opportunity for pupils to generate a large set of numbers, explore the many patterns and relationships that may be found and to make some generalisations.

Possible approach

As it is for the most able simply presenting the pupil with the activity as written may work well. Some learners may like to use materials to help to produce the sets of steps required.

If you and/or the pupil(s) are not used to working on investigations in this way, it may be helpful to read these articles and possibly discuss them with the Maths Subject Leader in your school.

Key questions

Tell me about the things you have found.
What ideas have you had to explore further?

Have you looked at Digital Roots?

Possible extension

These would have come come from the pupil(s), relating to things that have occurred during their investigation.

Possible support

Use of a spreadsheet may be appropriate.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Steps to the Podium