Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Round a Hexagon



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Round a Hexagon
Brenda is walking round an irregular hexagon (a shape with six straight sides). She starts off part of the way along one of the sides.
At each vertex (corner) she turns.
How much does she turn in total when she has walked all the way round?
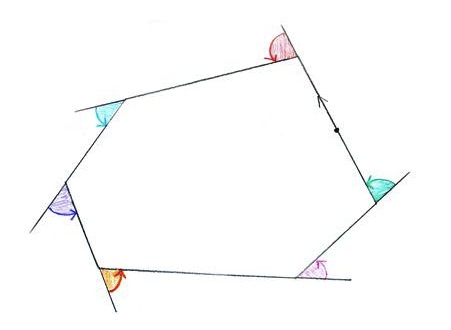
Use this example to prove that the sum of the external angles of any hexagon is $360$ degrees.
The external angle is found by extending the side and measuring the angle between the extended line and the next side.
Why do this problem?
This problem offers a geometric context for a generic proof. A generic proof works by using the structure of a particular example to show the result in the general case. In this case walking round any hexagon will involve turning through $360$ degrees. The external angles of the polygon are measured by extending the sides at each vertex and measured anticlockwise from the extension of the side to the adjacent side (see coloured angles below).
Possible approach
Get the children to draw hexagons in chalk on the playground. If they do this outside they can walk along the path themselves. They should start by facing along one of the lines on any of the sides. It is best to start part of the way along one side so that there is no confusion about the amount of turn involved to get to the same point facing the same way. When they get back to the starting point they will have turned through 360 degrees. It is important to turn in the same direction every time.
Key questions
Which way are you facing?How much have you turned?
How many turns are you making to go round the hexagon?
How much have you turned when you get back to where you started?
Possible extension
It would be possible to look at walking round different polygons in the same way. Polygons with reflex angles add an interesting twist to the thinking involved.
Possible support
More support could be offered through using a robot and programming it to go around a triangle or other polygon. The children may also find it helpful to use this worksheet. to explore the external angles in one hexagon. They could also draw their own hexagons, marking in the external angles and cut them up to fit the external angles together in the same way. The problem also links to Walking round a triangle. Cutting up a hexagon with the external angles marked on and fitting them together to form $360$ degrees gives an illustration of this result.
You may also like
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.

