Complex Squares

Ramana from Camilla Road Senior Public School has shown that if a complex number a+bi is not real, then it must be purely imaginary for its square to be a real number:

$(a+bi)^2 = a^2+2abi+(bi)^2$.
Suppose b is not 0. Then if a does not equal 0, the imaginary part of this, 2abi, will not be zero. So we must have $a = 0$.

Now the only term remaining is $(bi)^2$. This is equal to $b^2 *  i^2$, giving $-b^2$ which is a real number.

Example:
$(0+2i)^2 = -4$.

Robert James from Easingwold Secondary School has thought about this too, as well as which complex numbers square to give imaginary numbers:

If we say that $z + yi  (Z_2)$ is the square of $a +bi  (Z_1)$:
$z+yi = (a+bi)^2$
so $z+yi = a^2+2abi+(bi)^2$
and then $z+yi = a^2+2abi- ­b^2$
We can draw from this that $z=a^2 ­-b^2$ and $y=2ab$.
$Z_2$ will only be real when a or b is 0. This makes sense: as shown earlier z = $a^2 ­-b^2$ and $y=2ab$, so, for y to be zero (which we need because it is the coefficient of i) either a or b (or both) must be zero. Represented on an Argand diagram:



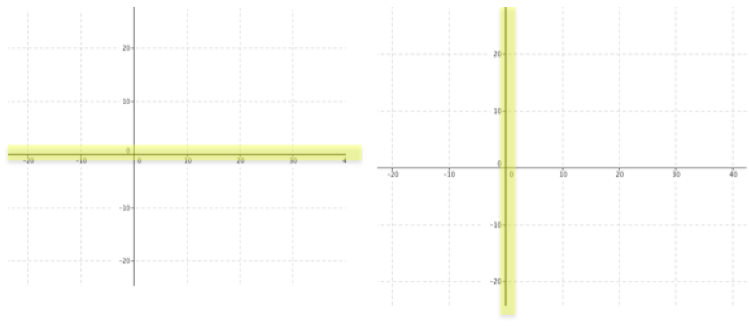
When a is zero, $a^2+2abi ­-b^2$ is reduced to $-b^2$, and when b is zero it is reduced to $a^2$. This means that if b is zero the squared number will be positive and if a is zero it will be negative.

For $Z_2$ to be imaginary a and b have to be equal or the negative version of the other. This is because the real part of $a^2+2abi-b^2$ is $a^2 -b^2$. So for this to equal zero, $a^2$ must equal $b^2$. On an Argand diagram:




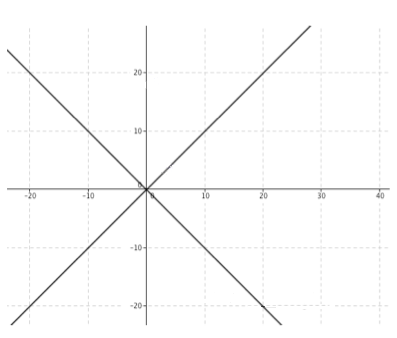
If a and b are equal, 2ab will be positive and so the imaginary coefficient will be positive. However, if one is the negative version of the other $2ab$ will be negative and so the coefficient will be too.

If you have any other solutions or conjectures to this problem, please send them in!