Skip over navigation


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Squaring the Rectangle
Age 14 to 18
Challenge Level 





Draw a rectangle on a piece of paper, and cut it out.
Can you find a way to cut your rectangle into pieces that can be reassembled to make a square?
Try to do it using the smallest number of pieces you can.
Is it always possible to cut up and reassemble a rectangle into a square using finitely many pieces?
Here are some suggestions to help you to think about this question:
Start with a rectangle with dimensions in the ratio 2:1. What side length do you need your square to have? How could you construct it?
Start with a square. How many different ways can you find to cut it into two pieces to make a rectangle? Or three pieces?
Click below to find an interactivity which shows one way of cutting up and reassembling a square to make a rectangle.
Can you move the pieces to make a square?
Can you move the pieces to make a rectangle?
Slide the point on the side of the square to change the pieces.
Move and rotate each piece using the blue dots.
Can you work out how the pieces were constructed?
Can you find a way to cut your rectangle into pieces that can be reassembled to make a square?
Try to do it using the smallest number of pieces you can.
Is it always possible to cut up and reassemble a rectangle into a square using finitely many pieces?
Here are some suggestions to help you to think about this question:
Start with a rectangle with dimensions in the ratio 2:1. What side length do you need your square to have? How could you construct it?
Start with a square. How many different ways can you find to cut it into two pieces to make a rectangle? Or three pieces?
Click below to find an interactivity which shows one way of cutting up and reassembling a square to make a rectangle.
Can you move the pieces to make a square?
Can you move the pieces to make a rectangle?
Slide the point on the side of the square to change the pieces.
Move and rotate each piece using the blue dots.
Can you work out how the pieces were constructed?
You may also like
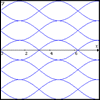
Sine Problem
In this 'mesh' of sine graphs, one of the graphs is the graph of the sine function. Find the equations of the other graphs to reproduce the pattern.
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.
The Frieze Tree
Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?

