Skip over navigation
Minh from BVIS in Vietnam sent an image of the pieces from the interactivity made into a square. This in Minh's image:
 (which comes from this rectangle)
(which comes from this rectangle)

Laiba from Doha College in Qatar made a beautiful poster with details of several different approaches.
Click here to see a larger version of Laiba's poster.
Minee & Pin M & Gor-Bua from Bangkok Patana School in Thailand and Ana also used a rectangle with dimensions in the ratio 2:1. Ana started with this rectangle:
The rectangle has length to width ratio $2:1.$ As an example the width is $1$ cm and the length is $2$ cm.


The area of the rectangle and square must be equal. In this case it must be $2$ cm$^2$. The square has equal length sides and therefore the sides will have length $\sqrt2$ cm.
If the second rectangle drawn is cut into four pieces, across the diagonal of each $1\times 1$ square which is shown right, then the length of diagonals will be $1^2+1^2=a^2$ and thus $a=\sqrt2.$
The yellow triangle's hypotenuse has length $\sqrt2,$ which is the [side] length of the square which will be constructed. A total of four yellow triangles can be cut out from the original rectangle and rearranged to create a square like this:

The triangles had length $ \sqrt2$ and two sides with length $1.$ The diagonal of the square is $2,$ which is equal to $2$ times $1$ cm, the width and half of the length of the previous rectangle.
This can be done with any triangle with ratio $2:1.$ Instead of the sides being $2$ and $1$ they can be called $a$ and $2a.$ The area of the rectangle and square would then be $2a^2.$ The sides of the square are $\sqrt2a.$
This formula can be [verified] with our example of sides $2$ and $1.$ If $1$ is $a$ then the sides of the square is $\sqrt2\ast1=\sqrt2$
Minee & Pin M & Gor-Bua proved that this formula works:
Because the lengths are "$a$" and "$2a$", to find the area of the rectangle you'll have to do $a \times 2a = 2a^2$
Because we are not cutting out any of the rectangle's area, the area of the square must be $2a^2$
To find the side lengths of the square you'll have to do $\sqrt{(2a^2)}$ because you have to do $x\times x$ to find the area ($x=\sqrt{(2a^2)}$).
David from LAE Tottenham in the UK generalised Min's method so that it will work for any rectangle:
Take any rectangle of size $a\times b$:

height $=a$
width $=b$ where $a$ and $b$ are positive and $\left \lfloor \frac {b}{a} \right \rfloor= 1$
Where $\left \lfloor x \right \rfloor$ means the highest whole number $n$ which is less than or equal to $x$ (i.e. $x$ rounded down to the nearest whole number).
 We cannot use this division of the rectangles when $\left \lfloor \frac {b}{a} \right \rfloor > 1,$ as if we do the same, we do not get a square:
We cannot use this division of the rectangles when $\left \lfloor \frac {b}{a} \right \rfloor > 1,$ as if we do the same, we do not get a square:
This process could be repeated $N$ times, and eventually $\left \lfloor \frac ba \right \rfloor =1,$ which means that it can be transformed into a square.
It should be done as follows:
1. Start with the rectangle of size $a \times b$ where $\left \lfloor \frac ba \right \rfloor > 1.$

2. Find the highest square number $n^2$ fitting into $b$ such that $\left \lfloor \frac an \right \rfloor =1$ or $\left \lfloor \frac na \right \rfloor =1.$ Divide $b$ into $n^2$ even lengths (Note $\frac b {n^2}$ doesn't have to be an integer), forming new rectangles ($n=2$ shown in example)

3. Perform the previous method on each rectangle, to get $n^2$ squares of area $\frac{ab}{n^2}:$

4. Rearrange the pieces to form squares:

each square has area $\frac{ab}{n^2},$ but there are $n^2$ squares, so the total area is still $ab^2$
5. Since there are $n^2$ squares, and $n^2$ is a square number, the rectangle can be rearranged into a square of area $ab$.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Squaring the Rectangle
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Minh from BVIS in Vietnam sent an image of the pieces from the interactivity made into a square. This in Minh's image:
 (which comes from this rectangle)
(which comes from this rectangle)Laiba from Doha College in Qatar made a beautiful poster with details of several different approaches.
Click here to see a larger version of Laiba's poster.
Minee & Pin M & Gor-Bua from Bangkok Patana School in Thailand and Ana also used a rectangle with dimensions in the ratio 2:1. Ana started with this rectangle:
The rectangle has length to width ratio $2:1.$ As an example the width is $1$ cm and the length is $2$ cm.
The area of the rectangle and square must be equal. In this case it must be $2$ cm$^2$. The square has equal length sides and therefore the sides will have length $\sqrt2$ cm.
If the second rectangle drawn is cut into four pieces, across the diagonal of each $1\times 1$ square which is shown right, then the length of diagonals will be $1^2+1^2=a^2$ and thus $a=\sqrt2.$
The yellow triangle's hypotenuse has length $\sqrt2,$ which is the [side] length of the square which will be constructed. A total of four yellow triangles can be cut out from the original rectangle and rearranged to create a square like this:

The triangles had length $ \sqrt2$ and two sides with length $1.$ The diagonal of the square is $2,$ which is equal to $2$ times $1$ cm, the width and half of the length of the previous rectangle.
This can be done with any triangle with ratio $2:1.$ Instead of the sides being $2$ and $1$ they can be called $a$ and $2a.$ The area of the rectangle and square would then be $2a^2.$ The sides of the square are $\sqrt2a.$
This formula can be [verified] with our example of sides $2$ and $1.$ If $1$ is $a$ then the sides of the square is $\sqrt2\ast1=\sqrt2$
Minee & Pin M & Gor-Bua proved that this formula works:
Because the lengths are "$a$" and "$2a$", to find the area of the rectangle you'll have to do $a \times 2a = 2a^2$
Because we are not cutting out any of the rectangle's area, the area of the square must be $2a^2$
To find the side lengths of the square you'll have to do $\sqrt{(2a^2)}$ because you have to do $x\times x$ to find the area ($x=\sqrt{(2a^2)}$).
David from LAE Tottenham in the UK generalised Min's method so that it will work for any rectangle:
Take any rectangle of size $a\times b$:

height $=a$
width $=b$ where $a$ and $b$ are positive and $\left \lfloor \frac {b}{a} \right \rfloor= 1$
Where $\left \lfloor x \right \rfloor$ means the highest whole number $n$ which is less than or equal to $x$ (i.e. $x$ rounded down to the nearest whole number).
 We cannot use this division of the rectangles when $\left \lfloor \frac {b}{a} \right \rfloor > 1,$ as if we do the same, we do not get a square:
We cannot use this division of the rectangles when $\left \lfloor \frac {b}{a} \right \rfloor > 1,$ as if we do the same, we do not get a square:This process could be repeated $N$ times, and eventually $\left \lfloor \frac ba \right \rfloor =1,$ which means that it can be transformed into a square.
It should be done as follows:
1. Start with the rectangle of size $a \times b$ where $\left \lfloor \frac ba \right \rfloor > 1.$

2. Find the highest square number $n^2$ fitting into $b$ such that $\left \lfloor \frac an \right \rfloor =1$ or $\left \lfloor \frac na \right \rfloor =1.$ Divide $b$ into $n^2$ even lengths (Note $\frac b {n^2}$ doesn't have to be an integer), forming new rectangles ($n=2$ shown in example)

3. Perform the previous method on each rectangle, to get $n^2$ squares of area $\frac{ab}{n^2}:$

4. Rearrange the pieces to form squares:

each square has area $\frac{ab}{n^2},$ but there are $n^2$ squares, so the total area is still $ab^2$
5. Since there are $n^2$ squares, and $n^2$ is a square number, the rectangle can be rearranged into a square of area $ab$.

You may also like
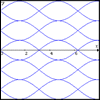
Sine Problem
In this 'mesh' of sine graphs, one of the graphs is the graph of the sine function. Find the equations of the other graphs to reproduce the pattern.
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.
The Frieze Tree
Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?

