Let Us Divide!

The solutions sent in made for interesting reading. Many pupils considered that because there were $8$ children coming to the party there were $8$ altogether. However Jola made it up to $9$. Swaathi in $5$k from the Garden International School in Malaysia was one of those but sent in a file that showed her interesting working as follows:


I started solving with the first problem that is:
It's Jola's birthday and she is having a party. She has $24$ cup-cakes to share equally between $3$ plates for the party. How many cakes will go on each plate?
My working out

Therefore, there are $8$ cup-cakes on each plate.
Next, I started with the second problem that is:
There are $8$ children coming to the party. They are all going to the cinema. How many cars will they need to take them there? Each car will hold $4$ children and they will each need a driver too.
My Answer and working out

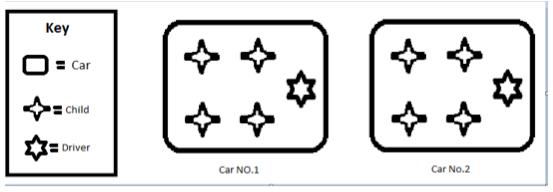
So, my answer is that there has to be two cars to go to the cinema.

Finally, I finished the last problem:
Jola is going to give everyone some chocolate eggs to take home at the end of the party. They fit into egg boxes which hold 6 eggs each. Will $50$ eggs be enough for each of the $8$ visitors to have a box to take home?
My Answer and working out

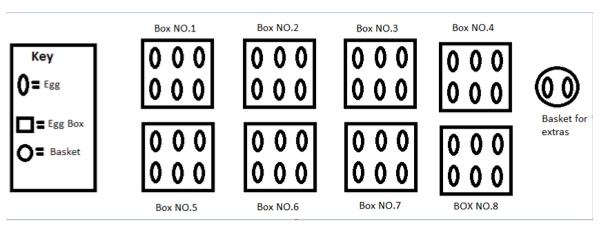
Every visitor will receive a box that contains $6$ eggs but as it is shown on the diagram, there will be $2$ eggs left over.

We also had solutions sent in that did consider that the eight visitors would make $9$ children altogether needing cars. These came from year $5$ at St Johns C of E Primary and pupils from 2/3/4 at HSPA in Australia. Thank you all very much.