Make Those Bracelets
Make Those Bracelets
Here are two pictures of children and parents in Africa making bracelets. They have lots of colourful beads to choose from.
Let's think about making a bracelet using two different colours of beads.
The smallest bracelet will have four beads and the largest will have ten beads.
The Challenge
Find some ways of arranging four beads and then five beads on the bracelets, each time using two colours. Be careful not to have any arrangements the same! These two will be counted the same, as they are both 3 of one colour and 2 of the other colour.
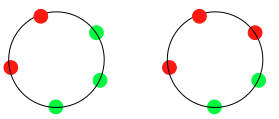
Try this next for six, seven, eight, nine and ten beads.
Final Challenge
A new person joins your group and wants to make bracelets.
Can you write down some guidance for them so that they have a system to make sure they find all the different arrangements and avoid repeats?
Why do this problem?
This activity engages the pupils in both a spatial and numerical context. It challenges their ability to see symmetrical reflections. It also gives them the freedom to choose how they go about the task - visualising in their head, using pencil and paper, beads, cubes or other counters that they have requested, and/or making use of a spreadsheet. They
can learn a lot from adopting one method and then realising that an alternative method might be better.
Possible approach
You could introduce the task as presented as on the problem page.
You may find it appropriate to make use of this interactive help
useful as part of designing the bracelets.
Key questions
Use open questions such as "tell me about this ..."
How did you decide on this approach to finding all the possibilities?
Possible extension
Explore the differences between this challenge and when the bracelets are like a non-reversable necklace.