Make Those Bracelets

Thank you to everybody who sent in their ideas about this task. There was some confusion over the rules - we have reworded the task slightly to hopefully make it clearer.

Landon from Dulwich College in Beijing, China worked out the possible numbers of each coloured bead on the bracelets:

If we have 4 beads in total: 2 + 2

If we have 5 beads in total: 2 + 3

If we have 6 beads in total: 2 + 4, 3 + 3

If we have 7 beads in total: 2 + 5, 3 + 4

If we have 8 beads in total: 2 + 6, 3 + 5, 4 + 4

If we have 9 beads in total: 2 + 7, 3 + 6, 4 + 5

If we have 10 beads in total: 2 + 8, 3 + 7, 4 + 6, 5 + 5

K from Crossflatts in the UK spotted that we are also allowed to have a bracelet which uses only one bead of one of the colours. K used this to find the different possibilities for 8 beads:

I think this is correct because I used number bonds to ten to find all of the sums but I was not allowed to use any number that included 0 and you couldn’t count two sums with the same numbers in it: 2+3=5 and 3+2=5 would only count as one. You use 2 different colours to represent the 2 numbers that add up to equal a certain number.

E.g. the bracelet could have 8 beads and my method is to find all the number bonds except any that includes 0 and the same numbers in 2 number sentences. So 4+4=8, 3+5=8, 2+6=8 and 1+7=8

Use this rule for 4,5,6,7,9 and 10 bead bracelets.

The children from Durham High School for Girls in the UK then used this information to work out the number of different arrangements for each number of beads. Some children felt that a bracelet with all the beads the same colour would be a possible solution, and some children didn't allow this.

Lara found these solutions for 4 and 5 bead bracelets:

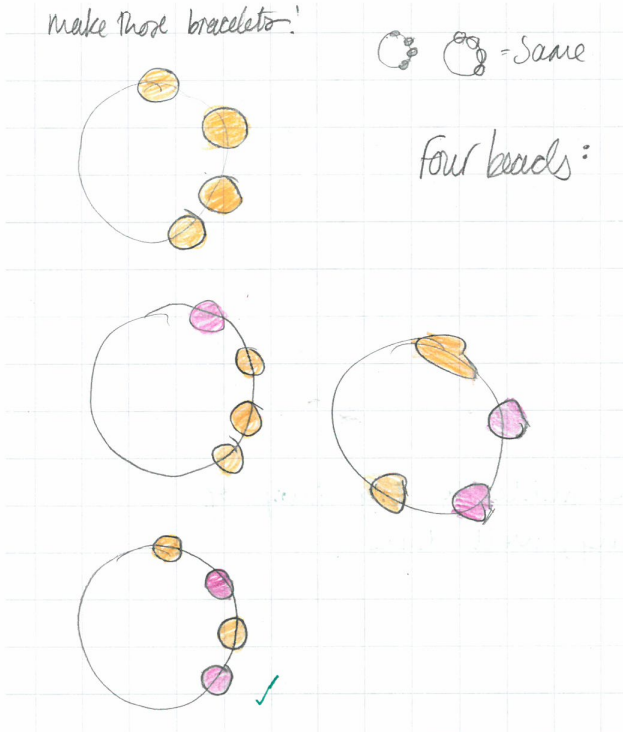
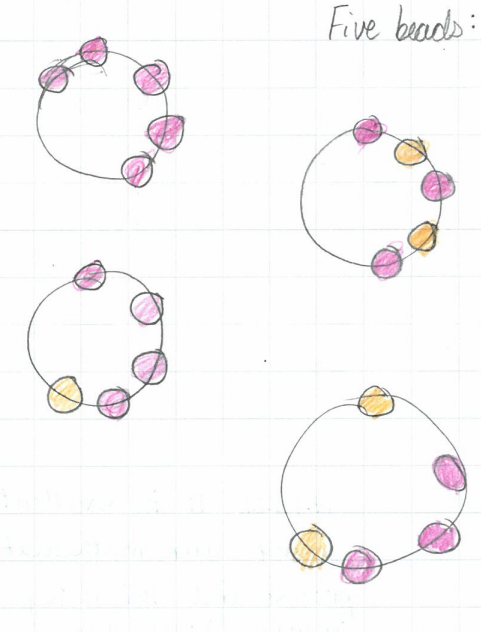
Thank you for sharing these pictures with us, Lara - these are all of the solutions for the bracelets with 4 and 5 beads.

Daniel from Exeter Cathedral School in the UK found a different way of recording the solutions instead of drawing pictures. Take a look at Daniel's full solution. It is very nearly a complete solution but Daniel has included some arrangements here that don't actually count as different arrangements, in bracelets which have the same number of beads of each colour. If anybody can spot Daniel's repeated arrangements, please email us to let us know.

Zara answered the question in the final challenge and gave some advice for anybody starting this activity:

Very hard! You have to try different patterns and arrangements. It takes a long time but it is fun! If you start from 1 it's easier. When you think you're done YOU'RE NOT, just keep trying different ones until you're finally done.

I'm glad you enjoyed it, Zara! This task is still open for solutions, so if anybody would like to try to work out how many possibilities there are then please do follow Zara's advice - start from a small number of beads and work your way up, then email us with your solution when you think you've found them all. Good luck!