Skip over navigation
Students from the Mathematics Extension Program (MEP) at Lumen Christi School in Australia sent in the following:-
Having previously attempted the Add Three Dice Challenge we were confident of finding multiple solutions to this problem.
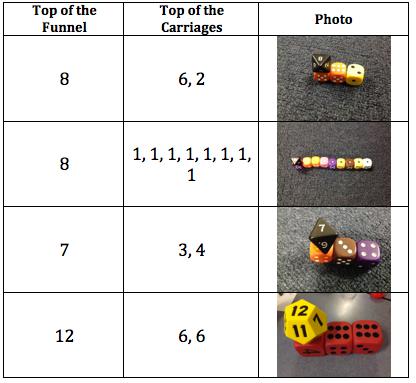
To begin we used different sized six-sided dice from around the Mathematics resource room and began trying various combination. After checking to see if each train met the two criteria we took a photo of the finished product.
After a while we decided to develop a recording system to ensure we were not repeating any combinations.
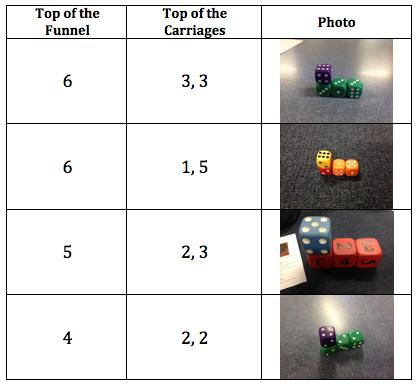
Hayden began investigating finding solutions that involved using more carriages. Soon other students took up this challenge.
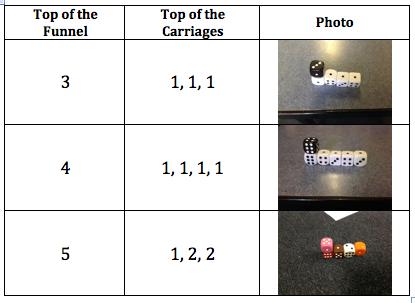
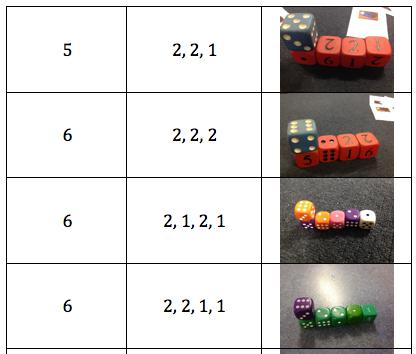
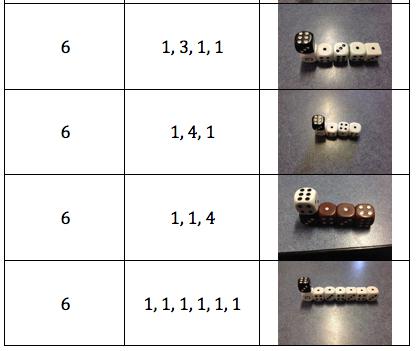
Hayden explained to the group that the final combination above: 6 - 1, 1, 1, 1, 1, 1 is the longest train that can be created using the initial criteria of having 6-sided dice.
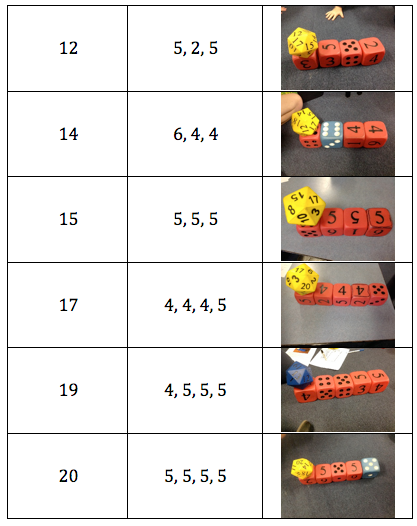
From here, students began to extend the problem by investigating whether or not they could find any solutions that still fulfilled the criteria, but used more dice or at least one dice that had more than 6 sides. Flynn was able to find and justify the first solution and soon other students followed. Flynn explained that under the black 8 is a 1, which matches with the 1 on the orange dice.
This suggestion prompted Jerusha to create a train that fulfilled the criteria, but had a wider funnel:
All up we found 18 solutions to the original problem and 14 solutions to different variations of the problem.
Thank you very much, an excellent thinking and well illustrated.
Haaziq Sheikh, Ethan Yu, Nanayaw Nyarko-Bonsu from Priorslee Primary Academy wrote:-
What we did.
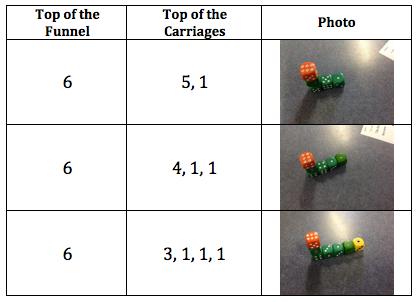
We got four dice and we focused on the last two carriages. So we had 3 and 2 connected with 1. We knew that the opposite numbers on all even dice add up to 7. As 7 minus 5 equals 2, we knew that the third dice had to have 2 on top and had to be connected by 6 because, as the other connection was 1, 7 minus 1 equals 6. Then we got 2 to connect with two of the odd
coloured dice and got 5 on top which is correct as 3 plus 2 equals 5.
We Learnt That:
opposite sides of a dice add up to 7
Thank you all of you for your submissions. If you've not tried this yourself have a go. You could follow the first solutions and start altering a rule to explore further.
The Dice Train
Age 7 to 11
Challenge Level 
Students from the Mathematics Extension Program (MEP) at Lumen Christi School in Australia sent in the following:-
Having previously attempted the Add Three Dice Challenge we were confident of finding multiple solutions to this problem.
To begin we used different sized six-sided dice from around the Mathematics resource room and began trying various combination. After checking to see if each train met the two criteria we took a photo of the finished product.
After a while we decided to develop a recording system to ensure we were not repeating any combinations.
Hayden began investigating finding solutions that involved using more carriages. Soon other students took up this challenge.
Hayden explained to the group that the final combination above: 6 - 1, 1, 1, 1, 1, 1 is the longest train that can be created using the initial criteria of having 6-sided dice.
From here, students began to extend the problem by investigating whether or not they could find any solutions that still fulfilled the criteria, but used more dice or at least one dice that had more than 6 sides. Flynn was able to find and justify the first solution and soon other students followed. Flynn explained that under the black 8 is a 1, which matches with the 1 on the orange dice.
Julian suggested we could make a train that met the criteria, but had a taller funnel.
This suggestion prompted Jerusha to create a train that fulfilled the criteria, but had a wider funnel:
All up we found 18 solutions to the original problem and 14 solutions to different variations of the problem.
Thank you very much, an excellent thinking and well illustrated.
Haaziq Sheikh, Ethan Yu, Nanayaw Nyarko-Bonsu from Priorslee Primary Academy wrote:-
What we did.
We got four dice and we focused on the last two carriages. So we had 3 and 2 connected with 1. We knew that the opposite numbers on all even dice add up to 7. As 7 minus 5 equals 2, we knew that the third dice had to have 2 on top and had to be connected by 6 because, as the other connection was 1, 7 minus 1 equals 6. Then we got 2 to connect with two of the odd
coloured dice and got 5 on top which is correct as 3 plus 2 equals 5.
We Learnt That:
opposite sides of a dice add up to 7
Thank you all of you for your submissions. If you've not tried this yourself have a go. You could follow the first solutions and start altering a rule to explore further.
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.