Going for Gold in 2012

I am breaking with tradition here and showing just one submission. We did also get solutions from St. John the Baptist School naming Tom, Niamh, Erin and Hayden, Kim, Abi and Laura, TC and Emily, Josh and Isobel, Ben and Oscar, Miah and Ali, Olivia and Eva, Joel Tom and Abigail, Kyle and Rio. We also had some good thoughts from Zain and Walail from St. Philips School, as well as Adam from Kings Chester. From Scotland  Nicholas and Angus  at St. Andrews.

So, from Ben Aditya and Megan at St. Nicolas School Newbury we had this grand submission.

Going for Gold
Ben H., Aditya and Megan from the Extension Maths Group.

The Extension maths group at St Nicolas CE Junior School, Newbury really enjoyed this problem. Our own country, Great Britain, was placed $4$th.  We looked on the internet and found out that there were $87$ countries listed in the complete $2008$ medal table and $204$ countries took part.
The positions have been decided on the amount of gold medals won by the country. Ben H thought there were better ways of doing it as the silver and bronze medal holders would be disheartened if it was just on gold because they wouldn't have helped their country in the medal table.
Aditya said it would be more fair to decide top place on the total number of medals because it judges second and third place as well.  The table would then look like this.

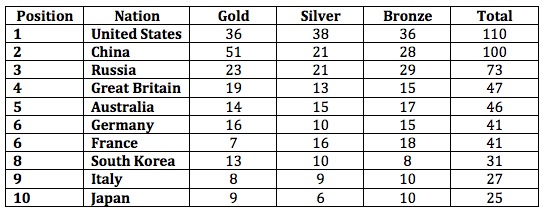
He noticed that:
* the top nation used to be China but now it's the United States;
* Russia and Great Britain stay in the same place;
* France has been lifted off the bottom up to sixth place with Germany.

Ben thought the best way would be to give $3$ points for a gold medal, $2$ for silver and $1$ for bronze because that would reward medals differently but everybody that won a medal would help their country move up the medal table.  Megan created the table:

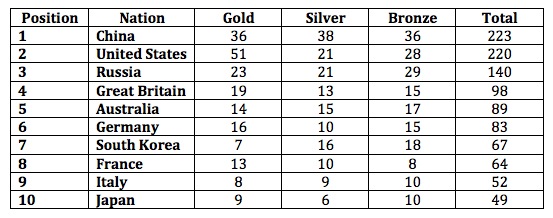
She noticed that with this method, compared to the given medal table, the top places are quite similar. The first four are the same but after that they begin to change more and more and by the time you've got to the bottom four, it is quite different.  Compared to Aditya's table, China is now top and South Korea and France have swapped places.

Well done all of you who sent in these thoughtful contributions. I hope to see your names again with next month's activities.