Skip over navigation
Swaathi from Brighton College Abu Dhabi sent in this excellent solution:
I started this problem by first identifying the different triangles within the 9-dot circle.
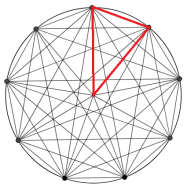
Let's figure out the red triangle's angles:
Since a circle has an interior angle of 360 degrees, we can divide 360 by 9 to give us one angle of the triangle. This is because the 9 dots are evenly spaced which means that all the red triangles are identical.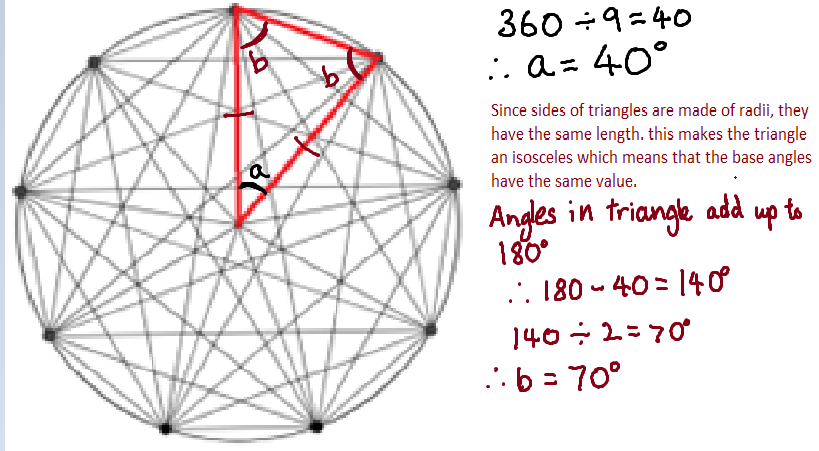
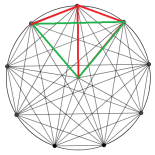
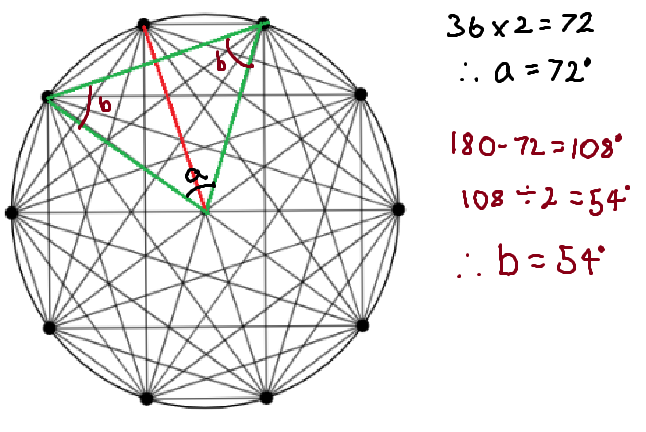
Now, let's look at the green triangle: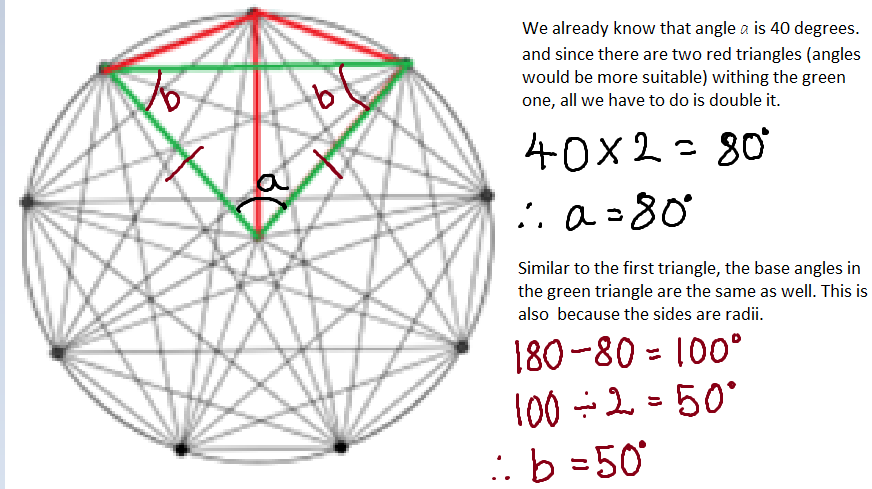
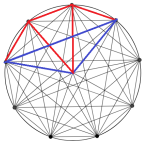
If we apply the same technique to the other triangles as well: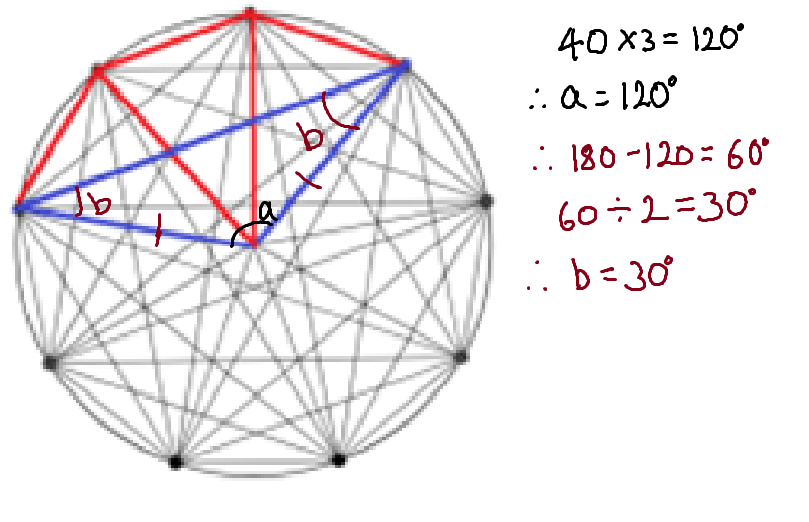
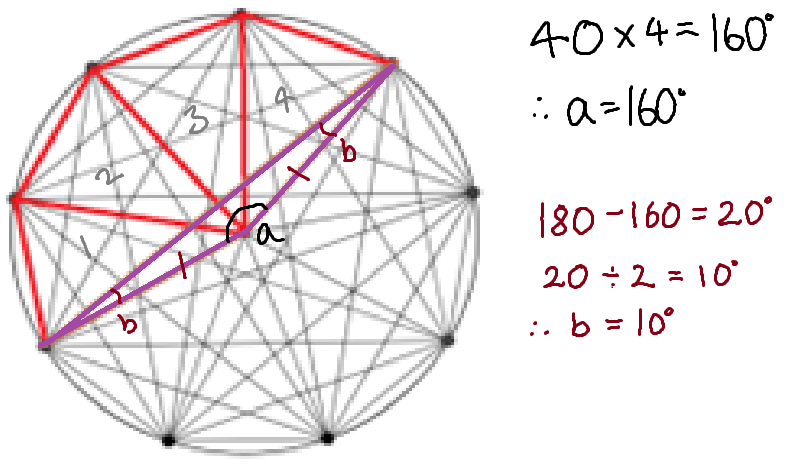
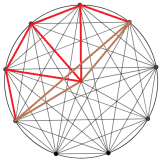
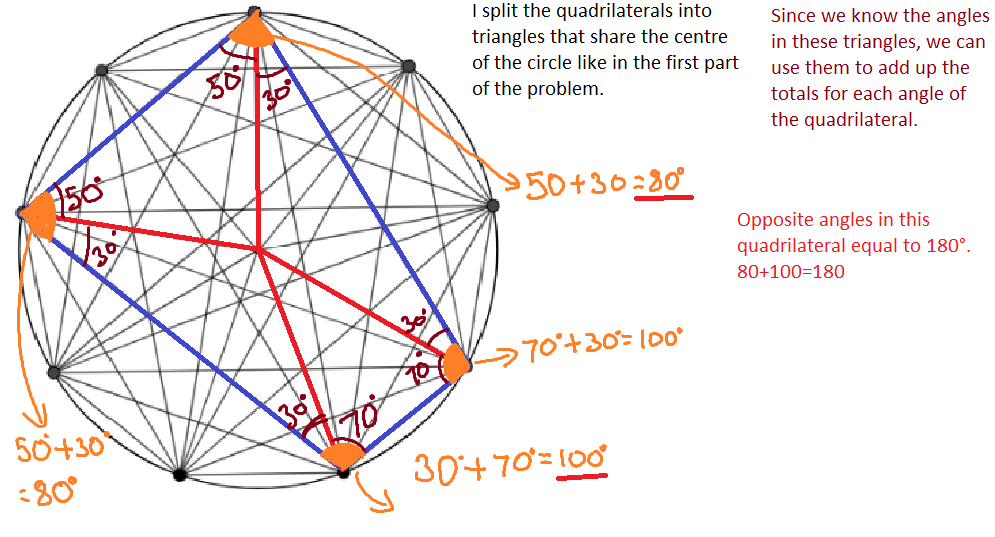
Now for the second part of the problem regarding quadrilaterals created using the points on the circumference of the circle.
I think that these methods can be applied to all the circles so in order to prove this theory I tested it with the 10 dot circle.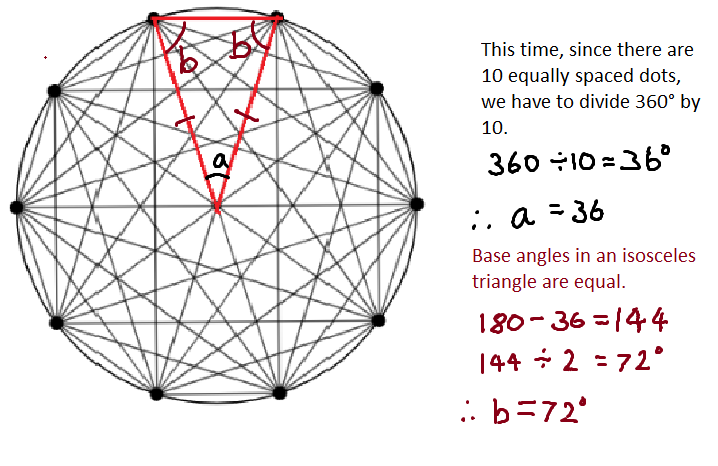
Extension:
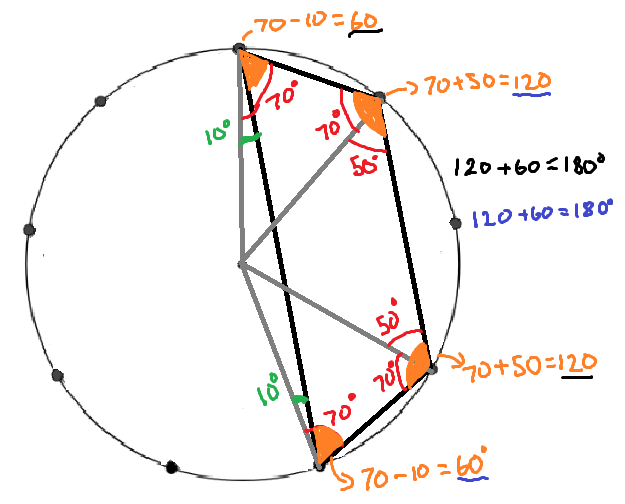
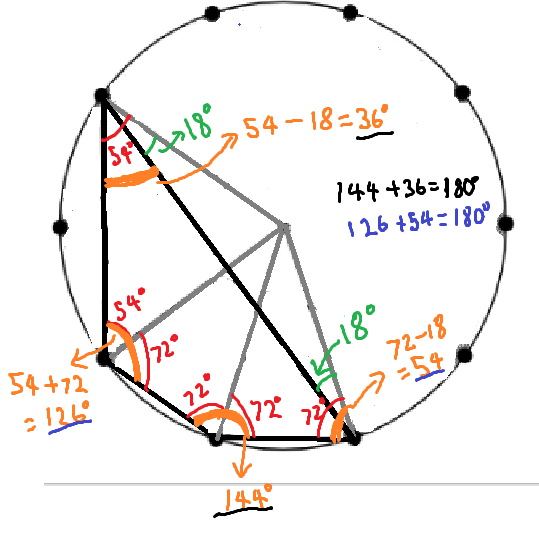
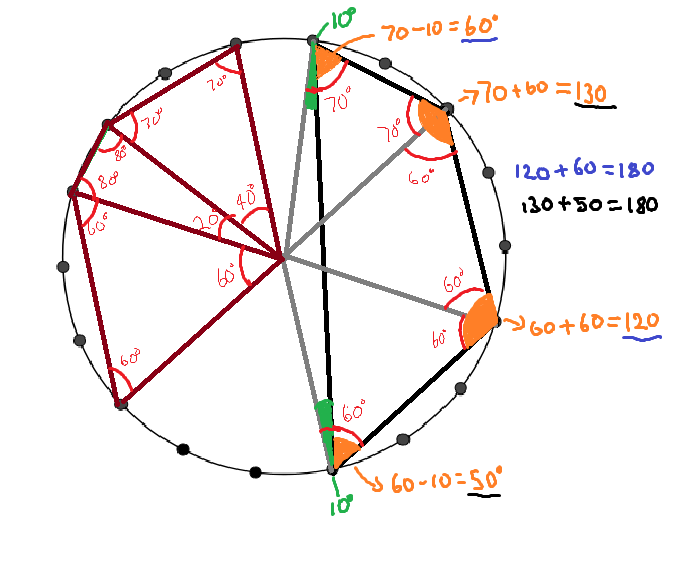
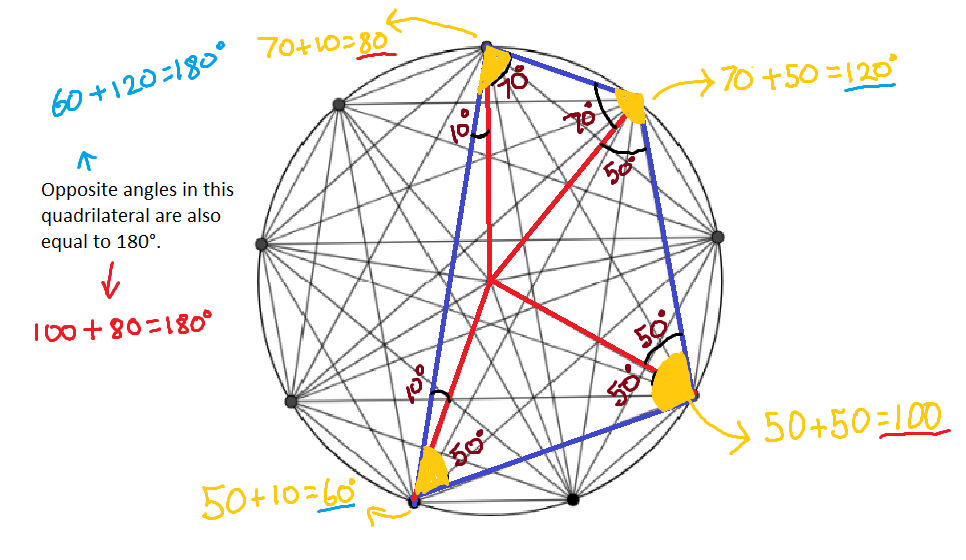
Swaathi claims that opposite angles in any quadrilateral within a circle add up to 180 °. Is this enough evidence to prove it?


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cyclic Quadrilaterals
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Swaathi from Brighton College Abu Dhabi sent in this excellent solution:
I started this problem by first identifying the different triangles within the 9-dot circle.




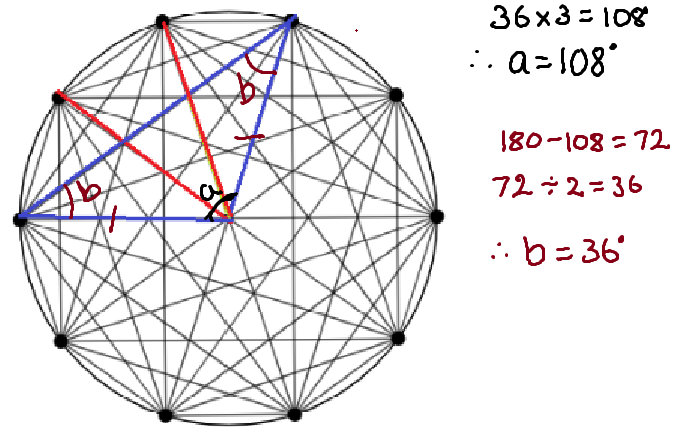
Let's figure out the red triangle's angles:
Since a circle has an interior angle of 360 degrees, we can divide 360 by 9 to give us one angle of the triangle. This is because the 9 dots are evenly spaced which means that all the red triangles are identical.

Now, let's look at the green triangle:

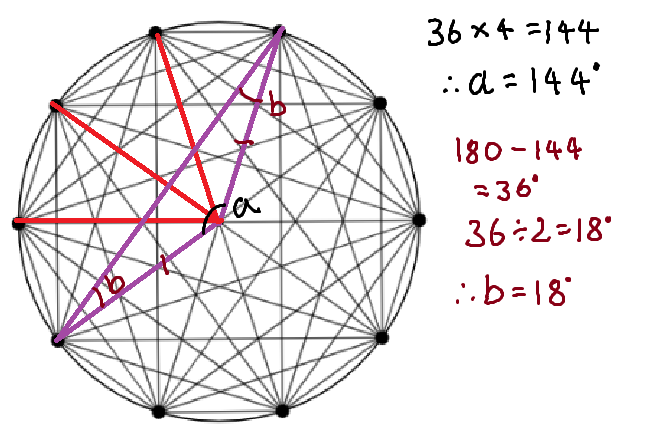
If we apply the same technique to the other triangles as well:


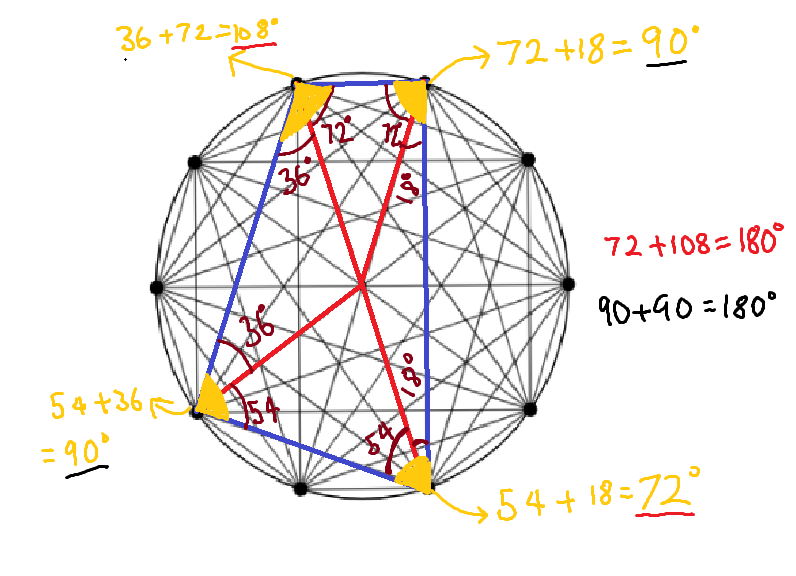
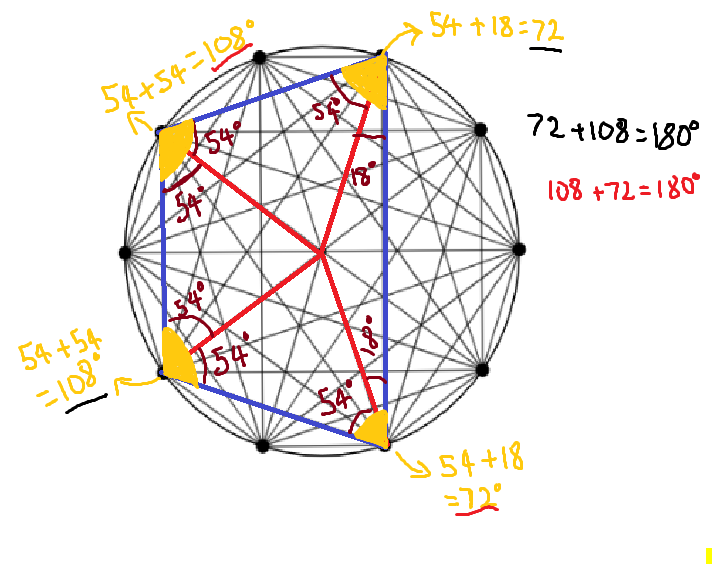
Now for the second part of the problem regarding quadrilaterals created using the points on the circumference of the circle.


I think that these methods can be applied to all the circles so in order to prove this theory I tested it with the 10 dot circle.






Extension:



Swaathi claims that opposite angles in any quadrilateral within a circle add up to 180 °. Is this enough evidence to prove it?
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?

