Skip over navigation
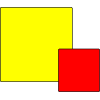
Luke from London Oratory School explained how the situation can be shown using algebra: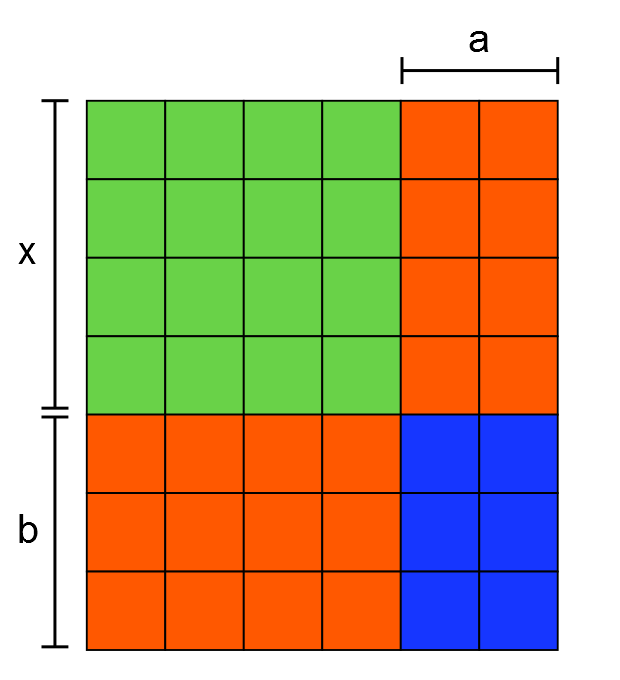 The green section is a square, so its area is equal to $x^2$.
The green section is a square, so its area is equal to $x^2$.
The red section (made of sticks) consists of two rectangles with dimensions $a, x$ and $b, x$. Therefore the red area is equal to $ax+bx$, which equals $x(a+b)$.
We can see that the area of the blue section will always have dimensions $a$ and $b$, so its area is equal to $ab$, if it Ê»ï¬llsʼ the gap created by the red area.
The total area is equal to the sum of these component areas.
Thus you can make a rectangle for all bases for expression of the form $x^2 + x(a+b) + ab$ where $a$ and $b$ are positive integers. The rectangle has dimensions $(x+a)$ by $(x+b)$.
1 square, lots of sticks and 12 or 100 units
Mahdi, Hamaad and Khalid used algebra again. Here is Mahdi's work for 12 sticks:
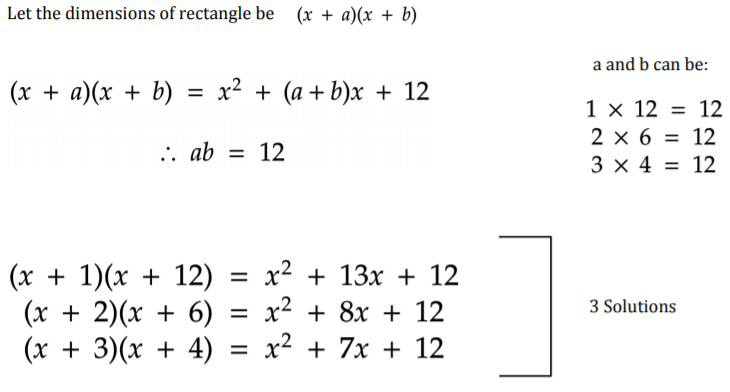
This is Hamaad and Khalid's work for 100 sticks:
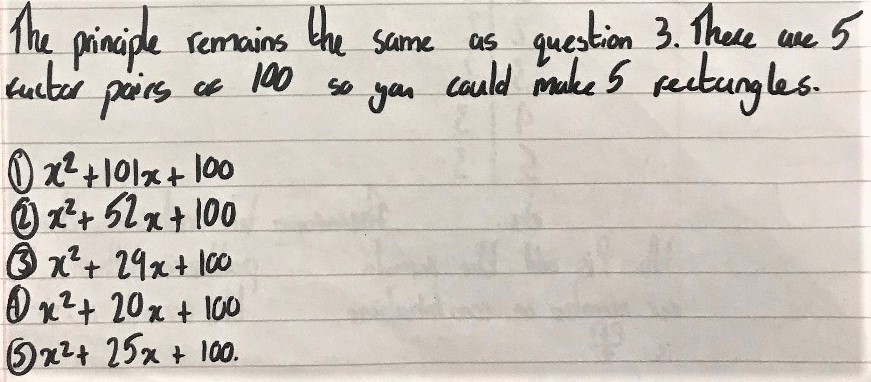
1 square, 12 or 100 sticks and lots of units
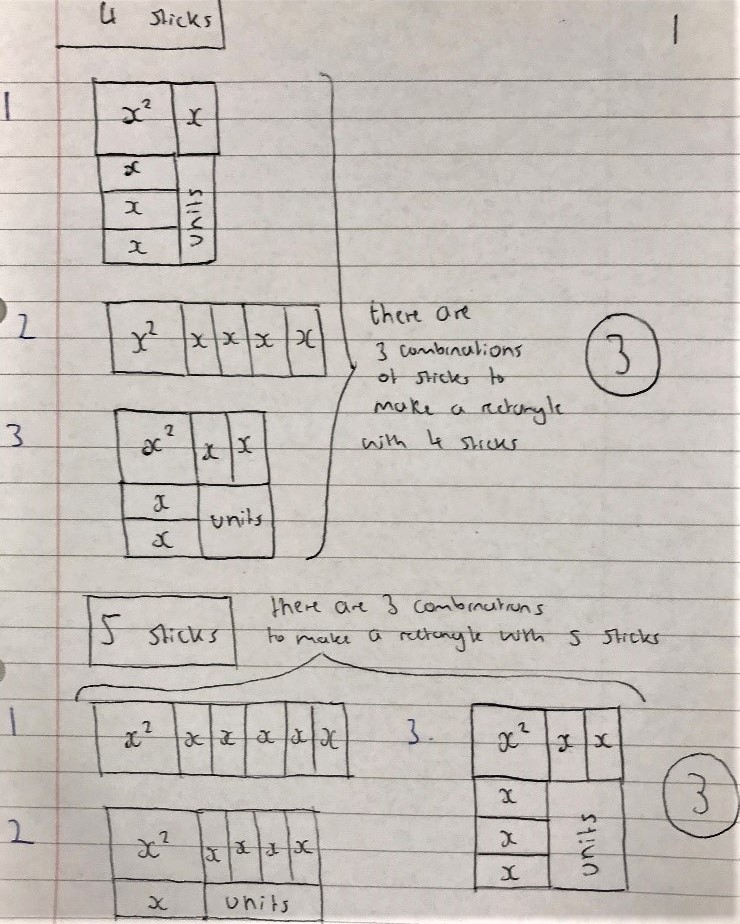
Hadi from Michaela Community School in the UK started with smaller numbers of sticks and then spotted a pattern:
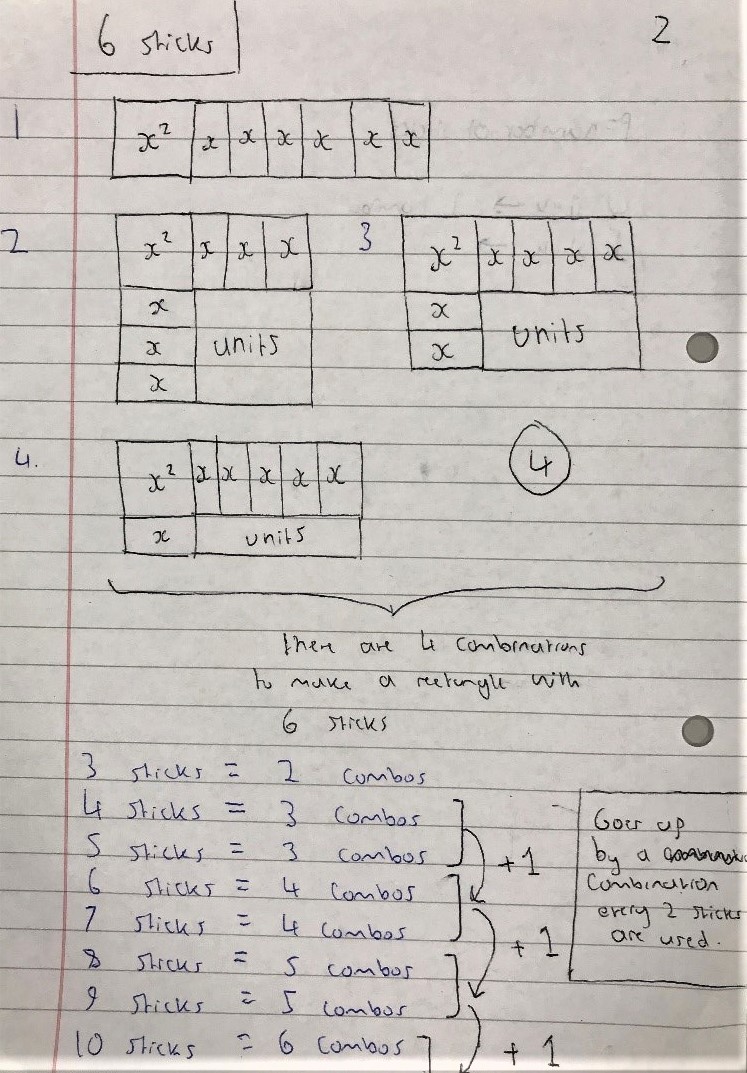

Mahdi from Mahatma Gandhi International School in India used algebra:

Hamaad and Khalid from Michaela Community School and Mahdi used the same approah for 100 sticks. This is Hamaad and Khalid's work:

For $p$ sticks and $q$ units
Mahdi approached this algebraically:
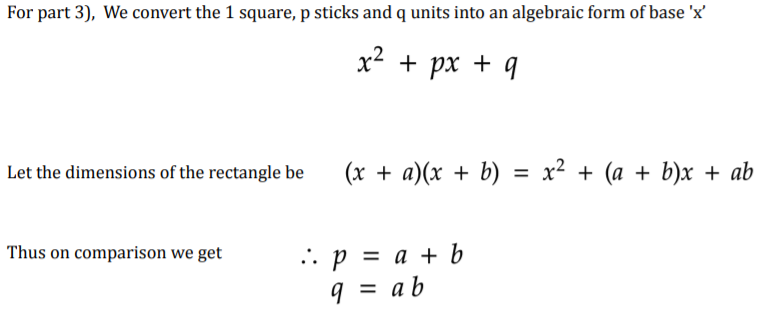
So how many different rectangles can you make with $p$ sticks and $q$ units?

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Factorising with Multilink
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Luke from London Oratory School explained how the situation can be shown using algebra:

The red section (made of sticks) consists of two rectangles with dimensions $a, x$ and $b, x$. Therefore the red area is equal to $ax+bx$, which equals $x(a+b)$.
We can see that the area of the blue section will always have dimensions $a$ and $b$, so its area is equal to $ab$, if it Ê»ï¬llsʼ the gap created by the red area.
The total area is equal to the sum of these component areas.
Thus you can make a rectangle for all bases for expression of the form $x^2 + x(a+b) + ab$ where $a$ and $b$ are positive integers. The rectangle has dimensions $(x+a)$ by $(x+b)$.
1 square, lots of sticks and 12 or 100 units
Mahdi, Hamaad and Khalid used algebra again. Here is Mahdi's work for 12 sticks:
This is Hamaad and Khalid's work for 100 sticks:
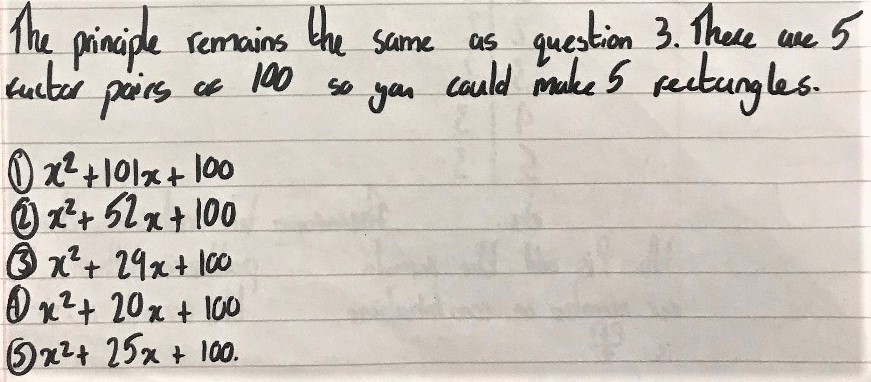
1 square, 12 or 100 sticks and lots of units
Hadi from Michaela Community School in the UK started with smaller numbers of sticks and then spotted a pattern:



Mahdi from Mahatma Gandhi International School in India used algebra:
Hamaad and Khalid from Michaela Community School and Mahdi used the same approah for 100 sticks. This is Hamaad and Khalid's work:

For $p$ sticks and $q$ units
Mahdi approached this algebraically:
So how many different rectangles can you make with $p$ sticks and $q$ units?
Related Collections
You may also like
Two Cubes
Two cubes, each with integral side lengths, have a combined volume equal to the total of the lengths of their edges. How big are the cubes? [If you find a result by 'trial and error' you'll need to prove you have found all possible solutions.]
Common Divisor
Find the largest integer which divides every member of the following sequence: 1^5-1, 2^5-2, 3^5-3, ... n^5-n.
Novemberish
a) A four digit number (in base 10) aabb is a perfect square. Discuss ways of systematically finding this number. (b) Prove that 11^{10}-1 is divisible by 100.

