Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Factors and Multiples Puzzle



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received many correct solutions to this puzzle:
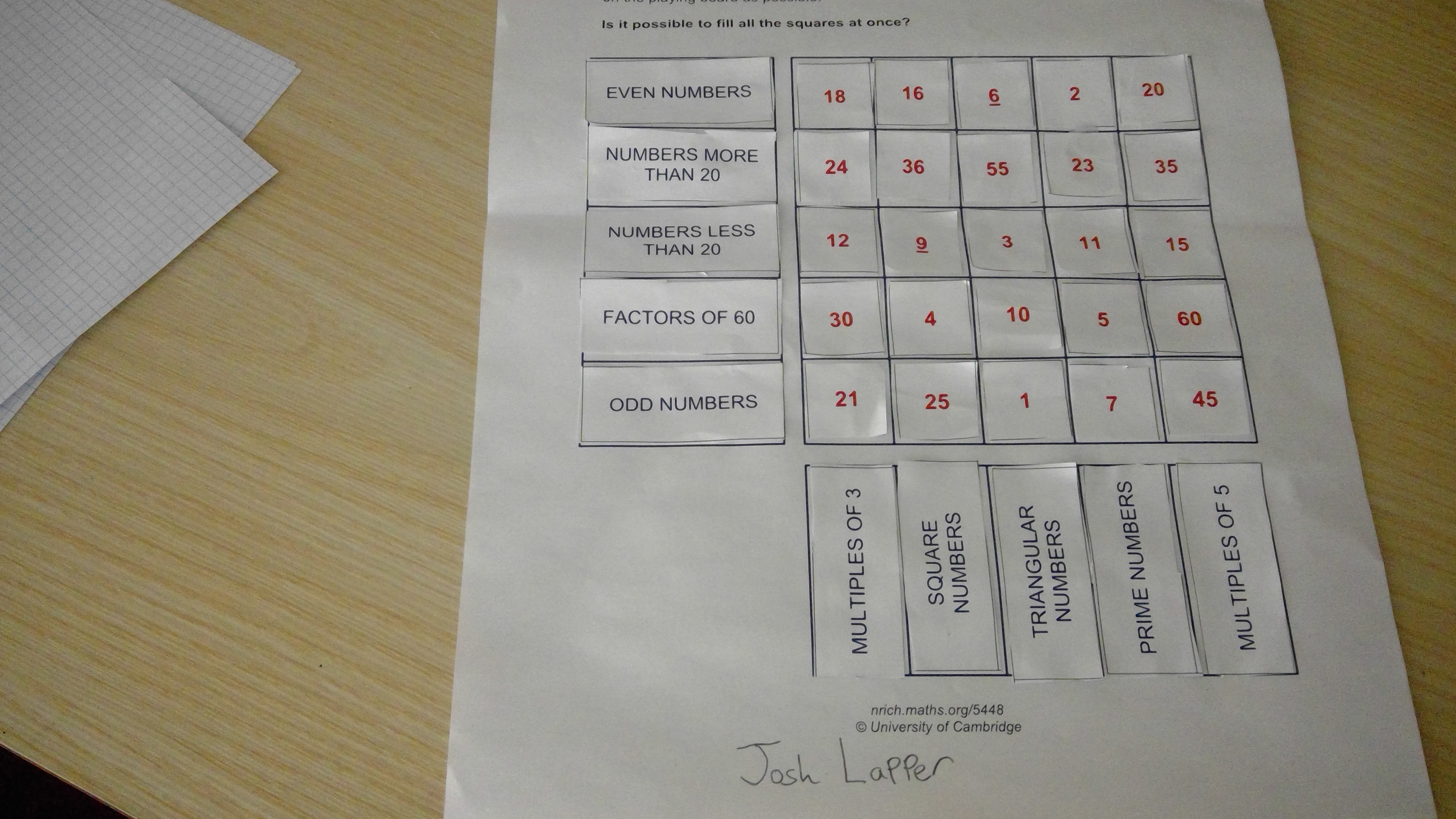
Josh from Swalcliffe Park School sent us this solution:
Elizabeth, Holly, Kelly, Harrison, Harry and Matthew from Miss Rowcliffe's Maths Class in Upton Heath C of E Primary School in Chester sent us this solution:
| Numbers less than 20 | 5 | 18 | 15 | 11 | 1 |
| Numbers more than 20 | 30 | 36 | 45 | 23 | 25 |
| Odd numbers | 35 | 21 | 55 | 7 | 9 |
| Even numbers | 20 | 24 | 10 | 2 | 16 |
| Factors of 60 | 60 | 12 | 6 | 3 | 4 |
|
Multiples
of 5
|
Multiples
of 3
|
Triangular
numbers
|
Prime
numbers
|
Square
numbers
|
Lydia from Woolmer Hill School sent in this solution:
| Numbers lesss than 20 | 16 | 1 | 18 | 15 | 7 |
| Numbers more than 20 | 25 | 30 | 60 | 35 | 23 |
| Odd numbers | 9 | 5 | 45 | 55 | 11 |
| Even numbers | 4 | 12 | 24 | 20 | 2 |
| Triangular numbers | 36 | 6 | 21 | 10 | 3 |
|
Square
numbers |
Factors
of 60
|
Multiples
of 3
|
Multiples
of 5
|
Prime
numbers |
Vicky and Katrina, also from Woolmer Hill School, submitted this solution:
| Numbers lesss than 20 | 4 | 18 | 6 | 10 | 11 |
| Triangular numbers | 1 | 21 | 15 | 45 | 3 |
| Odd numbers | 25 | 9 | 5 | 55 | 7 |
| Even numbers | 16 | 12 | 30 | 20 | 2 |
| Numbers more 20 | 36 | 24 | 60 | 35 | 23 |
|
Square
numbers
|
Multiples
of 3
|
Factors
of 60
|
Multiples
of 5
|
Prime
numbers
|
Ben, Henry, Joseph, Simon, Michael and Jake from Hampton School sent us these three different solutions.
Heidi, Lucy and Natasha from Millais School sent us this record of their work:
Initially we looked at the headings and found those that could not have any overlap,
e.g. Odd and evens, primes and square numbers, numbers under and over 20.
We placed those headings first and then put the others in place.
Here is their completed board.
Poppy and Hazel, also from Millais School, reported that:
We started by trial and error and got rather frustrated!
We realised that some of the headings had to be paired up because number could not appear in both categories, e.g. odds and evens, primes and squares.
From there we placed the headings in the table and gradually moved the others around until it worked. Interestingly, our solution was different to others in our class.
Lara and Jeni, again from Millais School, sent us a different solution
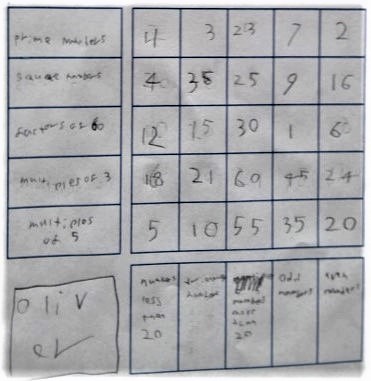
Oliver from Swalcliffe Park School in the UK sent in this solution:
Daniel and Marc, from the school Mirades of Barcelona, sent us their solution to the puzzle, with the headings in Catalan, together with their insights:
We had difficulties at first because we put the properties at random, and then we realized that we had to put greater and less than twenty in the same row, and even and odd too.

Congratulations also to Sam from Ridgewood School, Amy from SMTS and Polly and Heather from Hertfordshire and Essex High School who all sent us correct solutions. Well done to you all.
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!

