Fruity Totals

Why do this problem?

This interactivity provides an opportunity for students to become familiar with an unknown quantity being represented by a symbol and to begin developing the reasoning skills needed when manipulating algebraic expressions. For older students, it is an engaging context in which to practise solving simultaneous equations.

Often, when presented with a problem like this, some students may not be able to solve the problem in the time available.  As the interactivity can generate countless new grids, students can share their thinking about solution strategies and then use the insights they have gained to solve further examples. This supports students in becoming resilient problem solvers.
 

Possible approach

This activity featured in an NRICH student webinar in November 2021.

This task follows on from Different Deductions (for younger students) or What's it Worth? (for older students) which focus on the many different strategies that can be used to solve this type of problem.

Ideally, students would have access to computers or tablets so they can explore the interactivity with a partner. Give the class a short amount of time (five minutes or so) just to get used to the interactivity and 'play'. (See the article Using Digital Manipulatives and Interactivities to Develop Curiosity.) Bring them together and invite general comments or noticings and to address any misconceptions about the task.

"In a little while I'm going to stop you again and I want you to be able to explain a strategy that you have developed that helps you to find the values of the fruits."

Give the group some more time to work.  While they are working, circulate and listen out for good reasoning and useful strategies.  Each grid generated by the interactivity has a unique code, so if there is a particular grid that you would like to share with the whole class, you can access the code in the Settings menu. 
Click below to see a screenshot showing how to access the code in the Settings menu.

Access the Settings menu by clicking on the purple cog in the top right corner.
When you enter a code, you need to click on the box before re-starting the interactivity (the border of the box will become pink).

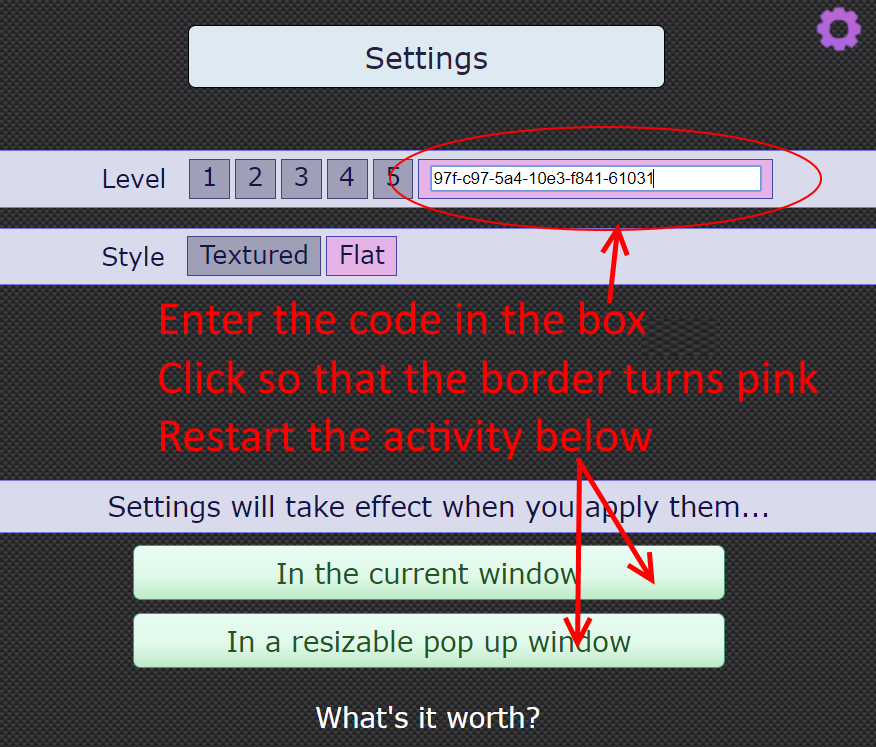
These are possible starting codes which usually generate plenty of discussion:

10d8-c28-590-91e-314c-64271

d6a-1151-8b7-975-7d84-04371

98c-ca1-928-4cf-56d4-64071

98a-d67-d5f-1088-de14-57202 (Level 2)

d5f-1147-925-52c-4d2c-50211

928-10ee-c3b-8c1-b748-26541

Bring the class together and invite students to share the strategies they have been using. Here are some examples of the sorts of strategies they might suggest:

The total of three apples and a cherry is 18 so I know that an apple is worth less than 6.

This row has two apples and two bananas so I can work out the value of apple+banana, and then use this to work out the value of a plum on the row that has two plums, an apple and a banana.

These two columns are the same except one has a cherry and one has an apple, so I can work out that a cherry is worth 2 more than an apple.

Having shared and discussed different strategies, give students an opportunity to put other people's strategies into practice. You may wish to do this by having everyone in the class work on the same example.

Key questions

Which row/s and/or column/s give you useful information?
Can you combine or compare rows and/or columns?
Which fruit is the easiest to work out the value of first?

Possible support

Trial and improvement is a strategy that will allow all students to access this task, although it would be good to encourage students to move towards more sophisticated strategies.

Possible extension

Once students are confident at solving Level 1 problems, there are four more levels for them to try, which can be accessed from the Settings menu. As the levels increase in difficulty, more of the row and column totals are hidden from the student so they have less information to solve the problem.