Fruity Totals

Children from Sheriffhales Primary School sent in the following (you can view larger versions on a new page by clicking the image)... 

From left to right, you can see Tom and Will's, Curtis',  Monty's and Joseph's solutions:
 

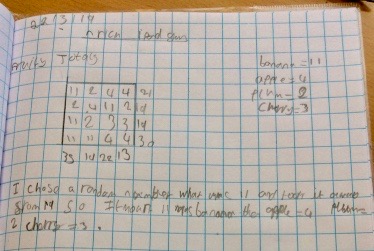
Lily May from St Ethelwold's in Wales wrote:

I used 'Explain Everything' to solve this problem and uploaded the video:



Mr G from Lily's school also gave this problem to his friends!

Kristin and Leslie from Westridge School For Girls in USA (California) sent in the following:

  


Isabelle from Skipton Girls' High School in the UK, Eric from the Biritsh School Manila in the Philippenes and Huu Huyen Tran from British Vietnamese International School in Vietnam used algebra.

Isabelle wrote:

Give each fruit a letter - apple ($a$), banana ($b$), cherry ($c$), plum ($p$).
Write out each sum using these letters. Find two lines with three of their fruits the same and write them as an equation:
eg. $1p+2a+1b+4=1p+1a+1c+1b$

simplify the equation
$1a+4=1c$

repeat this until you have a formula for each fruit
eg. $1b =1c+6$
      $1a=1c+3$
      $1p=1c+7$

pick any line and write it out using the formulas
eg. $2c+c+6+c+3=17$

simplify the equation and solve for $c$
$4c+9=17$
$c=2$

use this to work out other fruits
$c=2$, $a=5$, $b=8$, $p=9$