Less Is More
Less Is More
This is a game for two people, but is better played in two teams of two.
You will need a 1-6 or 0-9 dice. The interactivity here can be used to simulate throwing different dice.
Each team should draw some cells that look like the picture below. (The cells on the left don't need to be a different colour, but we will refer to those cells later.) Alternatively, you could print off this sheet of cells.
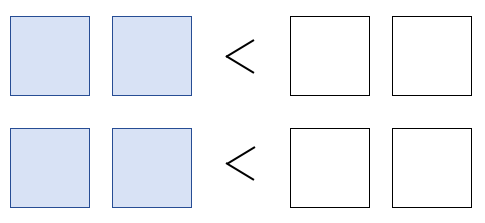
Version 1
You will need to throw the dice eight times in total. After each throw of the dice, each team decides which of their cells to place that number in.
When all the cells are full, each team will have created four two-digit numbers.
Teams then check if their number sentences are correct:
- If both number sentences are correct, the team scores the sum of the two two-digit numbers written in the blue boxes.
- If only the first number sentence is correct, the team scores the two-digit number in the top blue boxes.
- If only the second number sentence is correct, the team scores the two-digit number in the bottom blue boxes.
The winner is the team with higher score. See the hint for some examples of scoring.
Have a go at playing the game and keep a running total of your scores.
- Who is the winner after ten rounds?
- Who is the first to reach 500 points?
In between rounds, teams might like to find the highest possible score they could have achieved, if they had known the eight numbers in advance. These scores can be added to their running totals.
Will this affect your strategy in the next round?
Version 2
Now, imagine that the numbers 1, 2, 3, 4, 5, 6, 7 and 8 have been thrown.
Where would you place them in order to get the highest possible score?
Can you provide a convincing argument that you have arranged the numbers in the best possible way?
Have a go at playing the game just as you did in Version 1, but this time note down all eight dice rolls before deciding where to place them.
You can score in the same way as you did in Version 1. This time it could be the first to reach 1000 points who wins!
An interesting follow-up to this game is More Less is More, which again challenges you to create correct statements, but this time after carrying out some simple calculations.
Why play this game?
This game is thought-provoking and very engaging. It encourages discussion of place value, alongside valuable strategic mathematical thinking and it helps learners become more familiar with the mathematical symbols for 'greater than' and 'less than'.
Setting up the game with students working collaboratively with a partner offers the chance for them to focus on all five key ingredients that characterise successful mathematicians.
Possible approach
This problem featured in an NRICH Primary webinar in October 2020. It also featured in an NRICH Primary and Secondary webinar in November 2022.
This game can be played with a 1-6 dice or a decahedral 0-9 dice (interactive versions of dice and spinners are available here).
Invite volunteers (working in two teams of two) to play Version 1 of the game on the board. Explain that the aim is to fill the cells so that the statements are correct.
When the game is over, explain the scoring system and confirm who has won. Invite the whole class to work out the maximum score that would have been possible with the eight numbers that were rolled. Once you feel that learners have grasped the rules, set them off on playing the game, working in teams of two. Encourage learners to justify their strategies to their partners.
After each game, challenge teams to find the highest possible score they could have achieved, if they had known all eight rolled numbers in advance. Add these scores to their running totals and keep playing rounds of the game until one team has reached 500 (or 1000) points.
In the final plenary, challenge students to consider Version 2 of the problem (using the numbers 1-8). Encourage learners to use their knowledge of place value to make decisions, and challenge everyone to justify their reasoning, leaving no room for doubt.
Key questions
How are you trying to make sure each number sentence is true, while still managing to get a high score?
How are you deciding which cells to fill in first?
Possible extension
An interesting follow-up to this game is More Less is More, which again challenges learners to create correct statements, but this time after carrying out some simple calculations.
Possible support
Learners could try a single-digit version of the game initially, rolling the dice four times.
Learners could be provided with number cards that they can move around the grid to consider different options.
You may also like
Six Is the Sum
What do the digits in the number fifteen add up to? How many other numbers have digits with the same total but no zeros?
ABC
In the multiplication calculation, some of the digits have been replaced by letters and others by asterisks. Can you reconstruct the original multiplication?