Skip over navigation
This is Hope's method for finding the missing piece:
With the help of lego, I fiddled around with the puzzle pieces until I found a shape which almost finished the 3 x 3 area [volume] that the question asked for. So then I gathered extra lego blocks and softly placed them on the puzzle until I found the bricks that answered the solution.
Tim and Shahzaib from Greenacre Public School in Australia used a different method. Shahzaib wrote:
3 cubed equals to 27. That means the cube will be made of 27 blocks. If you add together the amount of blocks used in the picture, the answer will be 23. This means the sixth [piece] consists of 4 blocks.
So some people began by making different shapes from 4 small cubes.
Archie from Robert Hitcham primary school in the UK sent in a picture of two shapes which complete the puzzle:
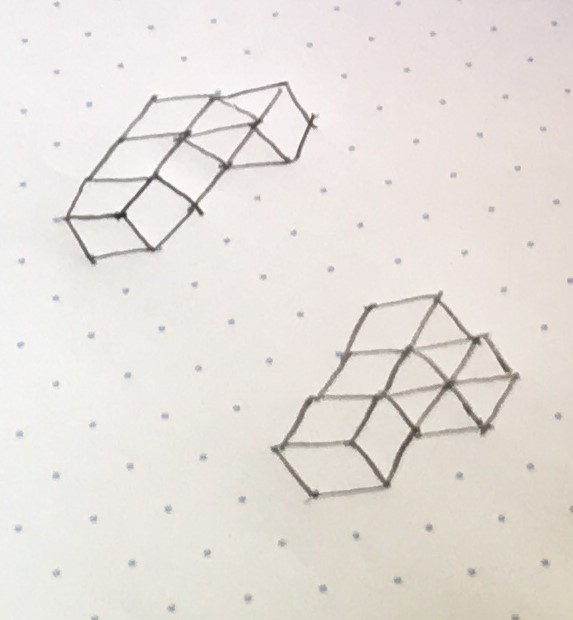
Click here to see a picture of Archie with his shapes.
James from Newington College in Australia sent this photo of the cube built from the pieces available with one of Archie's shapes missing:

Khan Vy from BVIS Hanoi in Vietnam sent this video of building the cube using the other one of Archie's shapes.
Nabiha and Gianna from Greenacre Public School described these two shapes and also one more:
Throughout trial and error we discovered that there are possible constructions in a T format, a L format and a 2 by 2 piece.
Van Khanh and Byung Kwon from BVIS Hanoi sent this video showing them building the cube using the "2 by 2 piece".
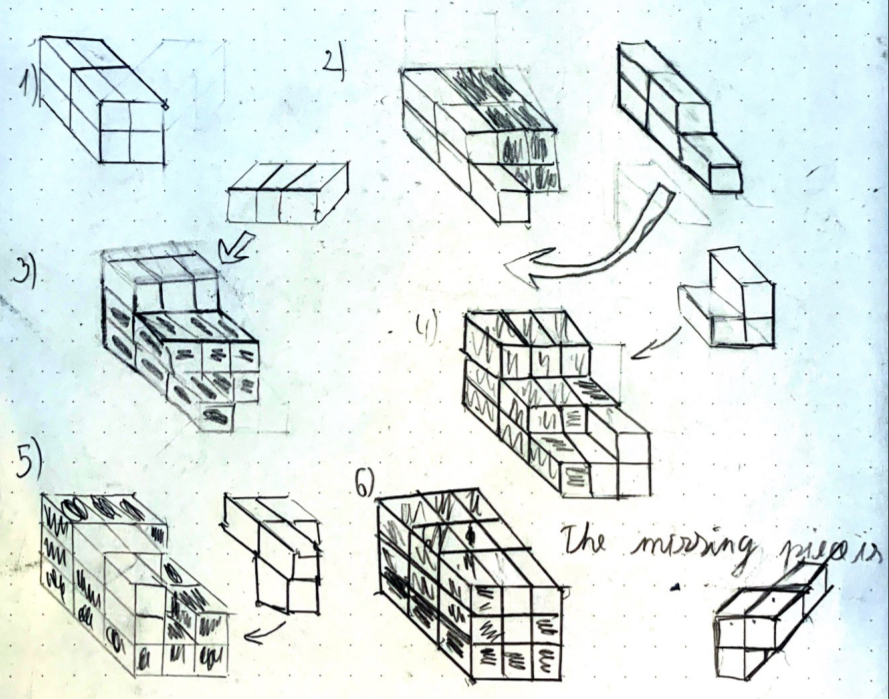
Michelangelo from Bangkok Patana Schol in Thailand found another solution:
I used the Lego instruction method. Every time I add a piece it is light and the old one is dark. I also draw the piece I am adding. I think there must be more solutions but this is my one.
Kimlan from BVIS in Vietnam sent this video of completing the cube using the same piece.
Renea, Barney, Olivia, Zara, Sylvie and Eve and Millie, Mia, Imtiaz and Shafin from North Chadderton School in Manchester, UK, found these 5 pieces which could finish the cube:

The T shape, the L shape and the 2 by 2 block are included, but Michelangelo's cube is not - so that makes a total of 6 ways to finish the 3 by 3 cube.
Those are all of the possible ways, unless we use this idea described by Oliver and Luke from North Chadderon School to make more:
We have noticed that sometimes the missing [piece] is a rotation of previous pieces we found - if we add the rotations we have 8 variations of the missing piece.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Nicola's Jigsaw
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This is Hope's method for finding the missing piece:
With the help of lego, I fiddled around with the puzzle pieces until I found a shape which almost finished the 3 x 3 area [volume] that the question asked for. So then I gathered extra lego blocks and softly placed them on the puzzle until I found the bricks that answered the solution.
Tim and Shahzaib from Greenacre Public School in Australia used a different method. Shahzaib wrote:
3 cubed equals to 27. That means the cube will be made of 27 blocks. If you add together the amount of blocks used in the picture, the answer will be 23. This means the sixth [piece] consists of 4 blocks.
So some people began by making different shapes from 4 small cubes.
Archie from Robert Hitcham primary school in the UK sent in a picture of two shapes which complete the puzzle:

Click here to see a picture of Archie with his shapes.
James from Newington College in Australia sent this photo of the cube built from the pieces available with one of Archie's shapes missing:

Khan Vy from BVIS Hanoi in Vietnam sent this video of building the cube using the other one of Archie's shapes.
Nabiha and Gianna from Greenacre Public School described these two shapes and also one more:
Throughout trial and error we discovered that there are possible constructions in a T format, a L format and a 2 by 2 piece.
Van Khanh and Byung Kwon from BVIS Hanoi sent this video showing them building the cube using the "2 by 2 piece".
Michelangelo from Bangkok Patana Schol in Thailand found another solution:
I used the Lego instruction method. Every time I add a piece it is light and the old one is dark. I also draw the piece I am adding. I think there must be more solutions but this is my one.
Kimlan from BVIS in Vietnam sent this video of completing the cube using the same piece.
Renea, Barney, Olivia, Zara, Sylvie and Eve and Millie, Mia, Imtiaz and Shafin from North Chadderton School in Manchester, UK, found these 5 pieces which could finish the cube:

The T shape, the L shape and the 2 by 2 block are included, but Michelangelo's cube is not - so that makes a total of 6 ways to finish the 3 by 3 cube.
Those are all of the possible ways, unless we use this idea described by Oliver and Luke from North Chadderon School to make more:
We have noticed that sometimes the missing [piece] is a rotation of previous pieces we found - if we add the rotations we have 8 variations of the missing piece.
You may also like
Soma - So Good
Can you mentally fit the 7 SOMA pieces together to make a cube? Can you do it in more than one way?
Nine Colours
Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?
Take Ten
Is it possible to remove ten unit cubes from a 3 by 3 by 3 cube so that the surface area of the remaining solid is the same as the surface area of the original?

