Nicola's Jigsaw

Why do this problem?

This problem offers students an opportunity to reason spatially in three dimensions, practise interpreting and drawing two dimensional representations of 3D shapes, and work systematically to find all the possible solutions to a problem.
 

Possible approach

The problem is much more manageable if students have cubes available to work with.
Introduce the problem and show students the diagrams of the five pieces:

     
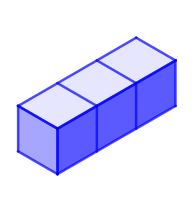
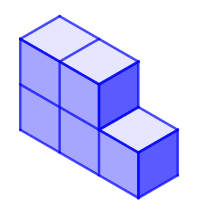
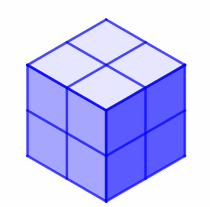
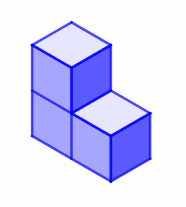
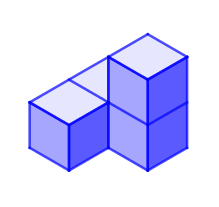
Some students might want to start by making the five pictured pieces.

In order to find what the missing piece might look like, encourage students to consider what they know about volume to deduce how many cubes make up the missing piece.

They could then make each possible missing piece to see if it can be used to complete the puzzle, and use isometric paper to record their findings. 

Nicola Coe has produced this revised version of her jigsaw puzzle, in which seven of the eight possible 4-block combinations can be used to complete the cube (the straight stick of 4 cubes can't fit in a 3x3x3 cube).
 

Key questions

What is the volume of each piece?
What is the volume of the finished puzzle?
What is the volume of the missing piece?
What possible shapes could the missing piece be?

Possible support

Students could work on The Third Dimension to practise working systematically and recording their work on isometric paper.

Possible extension

Nine Colours and Marbles in a Box offer suitable follow up challenges requiring reasoning in three dimensions.