Skip over navigation
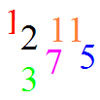
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Sets of Numbers
Age 7 to 11
Challenge Level 





How many different sets of numbers with at least four members can you find in the numbers in this box?

For example, one set could be multiples of $4$ {$8, 36 ...$}, another could be odd numbers {$3, 13 ...$}.
You may also like
Prime Magic
Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?
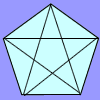
Diagonal Trace
You can trace over all of the diagonals of a pentagon without lifting your pencil and without going over any more than once. Can the same thing be done with a hexagon or with a heptagon?

