Skip over navigation
even numbers {$2, 8, 36, 56, 64, 136$}
odd numbers {$3, 13, 17, 27, 39, 49, 51, 91, 119, 121, 125, 143$}
multiples of one {all of them!}
multiples of $2$ {$2, 8, 36, 56, 64, 136$ - the same as even numbers!!}
multiples of $3$ {$3, 27, 36, 39, 51$}
multiples of $4$ {$8, 36, 56, 64, 136$}
multiples of $7$ {$49, 56, 91, 119$}
multiples of $8$ {$8, 56, 64, 136$}
numbers starting with $1$ {$13, 17, 119, 121, 125, 136, 143$}
square numbers {$36, 49, 64, 121$}
numbers containing $2$ {$2, 27, 121, 125$}
square roots {all of them are square roots !}
numbers containing $1$ {$13, 17, 51, 91, 119, 121, 125, 136, 143$}
numbers containing $6$ {$36, 56, 64, 136$}
cube numbers {$8, 27, 64, 125$}
numbers containing $3$ {$3, 13, 36, 39, 136, 143$}
prime numbers {$2, 3, 13, 17$}
numbers containing $9$ {$39, 49, 91, 119$}
numbers that you can subtract one from {all of them again!}
numbers between one and one hundred and forty four {all of them AGAIN!}
numbers between one and one hundred {$2, 8, 13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
whole numbers {all of them}
triple digit numbers {$119, 121, 125, 136, 143$}
numbers with double digits {$13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
We enjoyed this because we liked picking out different possibilities and seeing if they worked out. We could have submitted more but the bell rang! Thanks for the great challenge.
multiples of $17$: {$17, 51, 119, 136$}
... and multiples of $1$ which of course is all of the numbers.
Jin and Anushkawho go to Dubai International Academy had one more set:
digits add to $8${$8,17,125,143$}
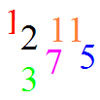
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Sets of Numbers
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Children from Beaumaris North Primary School, Melbourne told us:
In our Year 3 Enrichment group we discussed all the possible sets that could be found. Here is what we found!even numbers {$2, 8, 36, 56, 64, 136$}
odd numbers {$3, 13, 17, 27, 39, 49, 51, 91, 119, 121, 125, 143$}
multiples of one {all of them!}
multiples of $2$ {$2, 8, 36, 56, 64, 136$ - the same as even numbers!!}
multiples of $3$ {$3, 27, 36, 39, 51$}
multiples of $4$ {$8, 36, 56, 64, 136$}
multiples of $7$ {$49, 56, 91, 119$}
multiples of $8$ {$8, 56, 64, 136$}
numbers starting with $1$ {$13, 17, 119, 121, 125, 136, 143$}
square numbers {$36, 49, 64, 121$}
numbers containing $2$ {$2, 27, 121, 125$}
square roots {all of them are square roots !}
numbers containing $1$ {$13, 17, 51, 91, 119, 121, 125, 136, 143$}
numbers containing $6$ {$36, 56, 64, 136$}
cube numbers {$8, 27, 64, 125$}
numbers containing $3$ {$3, 13, 36, 39, 136, 143$}
prime numbers {$2, 3, 13, 17$}
numbers containing $9$ {$39, 49, 91, 119$}
numbers that you can subtract one from {all of them again!}
numbers between one and one hundred and forty four {all of them AGAIN!}
numbers between one and one hundred {$2, 8, 13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
whole numbers {all of them}
triple digit numbers {$119, 121, 125, 136, 143$}
numbers with double digits {$13, 17, 27, 36, 39, 49, 51, 56, 64, 91$}
We enjoyed this because we liked picking out different possibilities and seeing if they worked out. We could have submitted more but the bell rang! Thanks for the great challenge.
Olly from North Molton Primary also found:
multiples of $13$: {$13, 39, 91, 143$}multiples of $17$: {$17, 51, 119, 136$}
... and multiples of $1$ which of course is all of the numbers.
Jin and Anushkawho go to Dubai International Academy had one more set:
digits add to $8${$8,17,125,143$}
Can you find any more? How about triangle numbers and tetrahedral numbers?
You may also like
Prime Magic
Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?
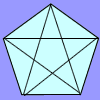
Diagonal Trace
You can trace over all of the diagonals of a pentagon without lifting your pencil and without going over any more than once. Can the same thing be done with a hexagon or with a heptagon?

