Hollow Squares
Hollow Squares printable worksheet
In Napoleonic battles a hollow square was a popular formation for an infantry battalion designed to cope with Cavalry charges.
For example, the picture on the right shows a recreation of Wellington's army at Waterloo.
Below are two diagrams showing symmetrical hollow square formations.
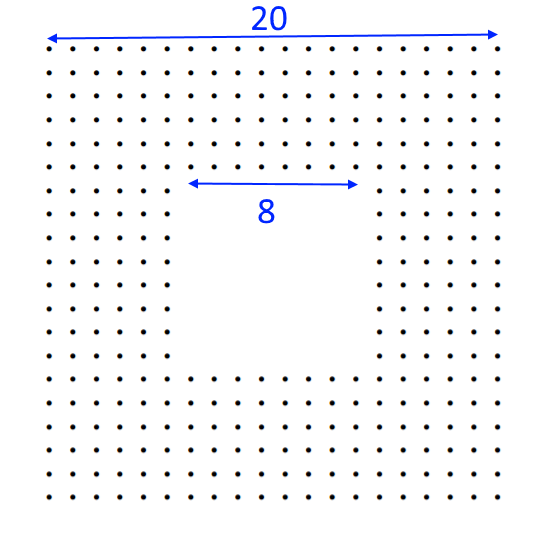
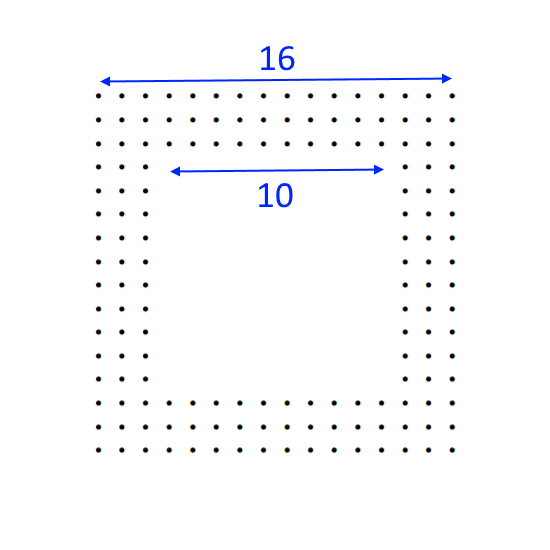
Click below to see two methods of dividing up the dots that might help you work it out:
Alison's Method:
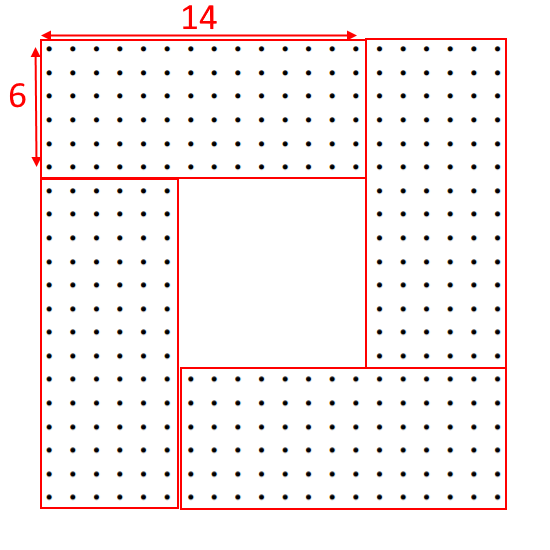
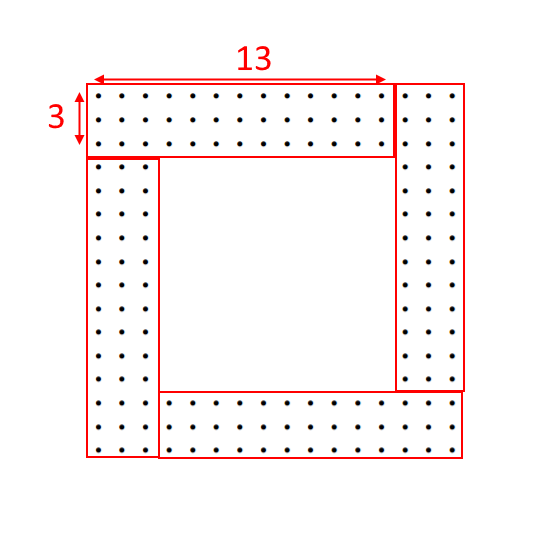
Charlie's Method:
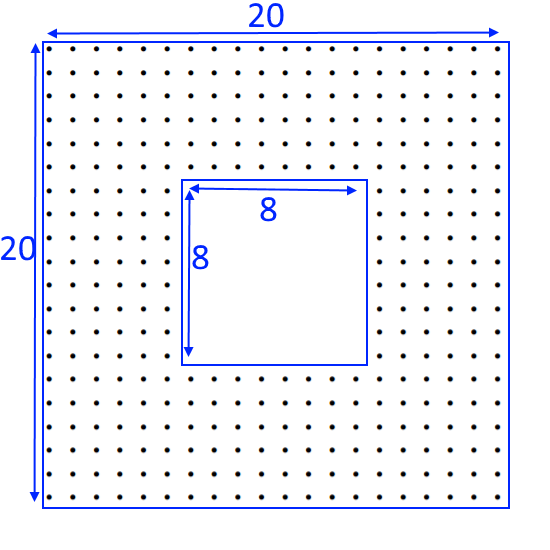
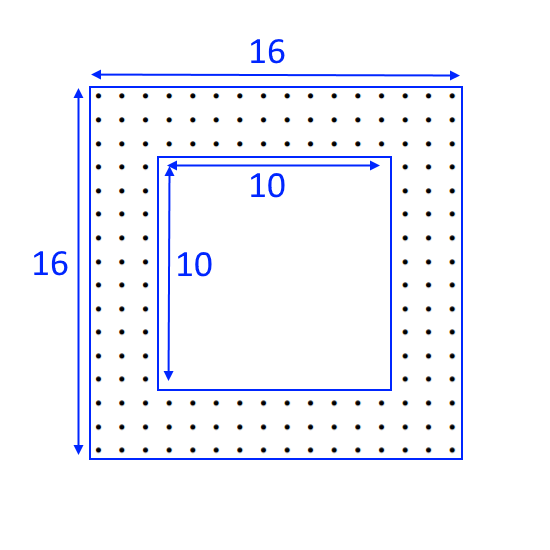
A general has 960 soldiers. How many different ways can he arrange his battalion in a symmetric hollow square?
What can you say about battalion sizes that can't be arranged as symmetric hollow squares?
Can you find a general strategy for arranging any possible battalion into all possible symmetric hollow squares?
What about hollow squares that are not symmetric...?
You may also like to take a look at What's Possible?
With thanks to Don Steward, whose ideas formed the basis of this problem.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.