Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Published 2014 Revised 2021
Reasoning: the Journey from Novice to Expert (Article)
This article forms part of our Reasoning Feature, and complements the article Reasoning: Identifying Opportunities.
Developing reasoning skills with young learners is a complex business. They need to learn to become systematic thinkers and also acquire the ability to articulate such thinking in a clear, succinct and logical manner. In many classrooms more progress is being made with developing the systematic thinking than with the elegant communication. There needs to be equal emphasis on both these aspects of
reasoning and in both we need to consider progression. What would we expect from a novice reasoner as opposed to an expert reasoner? How can we help young learners to progress to expert level?
Progression in reasoning
At NRICH we see a five-step progression in reasoning: a spectrum that shows us whether children are moving on in their reasoning from novice to expert. Children are unlikely to move fluidly from one step to the other, rather flow up and down the spectrum settling on a particular step that best describes their reasoning skills at any one time.
Step one: Describing: simply tells what they did.
Step two: Explaining: offers some reasons for what they did. These may or may not be correct. The argument may yet not hang together coherently. This is the beginning of inductive reasoning.
Step three: Convincing: confident that their chain of reasoning is right and may use words such as, 'I reckon' or 'without doubt'. The underlying mathematical argument may or may not be accurate yet is likely to have more coherence and completeness than the explaining stage. This is called inductive reasoning.
Step four: Justifying: a correct logical argument that has a complete chain of reasoning to it and uses words such as 'because', 'therefore', 'and so', 'that leads to'...
Step five: Proving: a watertight argument that is mathematically sound, often based on generalisations and underlying structure. This is also called deductive reasoning.
Let's look and see what these can look like in some children's solutions to an NRICH problem: Sealed Solution.
We need to bear in mind that when looking at these solutions we are assuming that children are able to communicate their thinking in a written form that is understandable by another without any verbal interpretation from the child themselves. In the classroom we are more likely to find out about children's reasoning through listening to their talk as they explore a mathematical challenge or
talking with them ourselves.
Here is the task Sealed Solution:

What numbers could be inside the "8" envelope?
Here's a solution that was sent to us from Ieuan in Prague:
At first I was randomly picking numbers, and on my first attempt doing it I found a solution:
0 + 7=7 5 + 3=8 9 + 4 =13 6 + 8=14 2 + 1=3.
And then I tried using a system from then on, of adding a number to the smaller number then subtracting one from the smaller number, but it did not go very well because when I converted 5 + 3 to 4 + 4 I realised that you cannot do that.
Then I found out something quite clever that from one onward: each 2 numbers have the same amount of possibilities (I think by this Ieuan means that pairs of consecutive numbers have the same number of possibilities). For example 2 and 3 have two possibilities, 4 and 5 have have three, 6 and 7 have four, 8 and 9 have five and it goes on forever! So I wrote
down all the possibilities for 7, 8, 13, 14, 3.
Then I shortened it, so if I use 13 as an example: 13+0, 12+1, 10+3, 9+4, 8+5, 7+6. Then I would take off 13+0, 12+1 and 10+3 and do that for all the rest! So when I had all the possibilities I did two attempts without succeding then I got one and I started explaining it on here, but I realised I had found the same as my first attempt.
Then I did one attempt and I found another: 3+0, 8+6, 9+4, 7+1 and 2+5.
We would say that this child is showing some reasoning ability as they describe how they move from a random approach to a more systematic approach. He uses phrases such as, 'I found the same as my first attempt' and shows how he moved to spotting a pattern: 'each two numbers have the same amount of possibilities'. However, he is not yet at the stage of being able to explain his reasoning
clearly - he says he thought it would be best to make the biggest totals first yet the reason is not given. His reasoning ability would seem to be ahead of his communicating ability, which is very common in young learners.
How does that first solution compare with this next solution to the same problem?
Year 6 pupils from St John Fisher Harrogate Magic Maths Club:
We started off by thinking of all the possible ways of making the totals. This took a long time.
We thought that it would be best to make the biggest totals first, using the bigger numbers to make them:
14 = 9 + 5, 13 = 6 + 7, 1 + 2 = 3, 4 + 3 = 7 and 8 + 0 = 8.
Some of us did it the other way round, making the smallest totals first, with the smallest numbers:
1 + 2 = 3, 4 + 3 = 7, 8 + 0 = 8, 7 + 6 = 13 and 9 + 5 = 14.
We could also come up with pairs randomly but it's quicker to use a strategy.
7 + 0 = 7, 5 + 3 = 8, 9 + 4 = 13, 6 + 8 = 14 and 1 + 2 = 3.
Like Ieuan the way that these children describe their problem-solving process suggests that they are developing some reasoning fluency: 'we thought that it would be best to make the biggest totals first, using the bigger numbers to make them'. However, they have yet to offer an explanation as to why they chose to do that.
Let's look at Rebekah's explanation for Sealed Solution and see how well she is beginning to justify her choices:
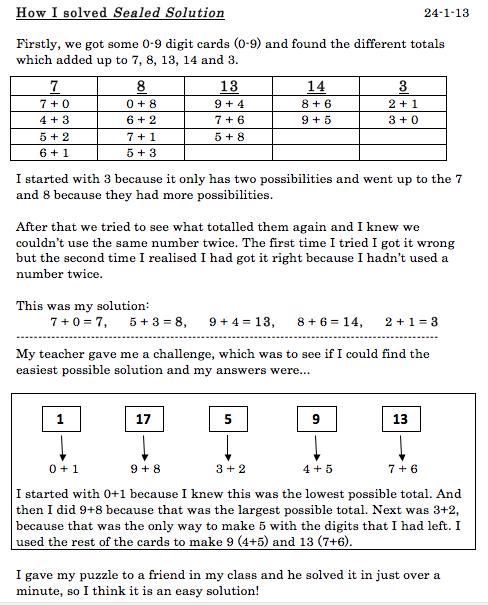
Rebekah uses phrases like, 'I started with the three because it has only two possibilities'. She is giving a reason for her choice yet still has to justify why this is a strategic choice. It is interesting to reflect on the difference between convincing and justifying. Convincing can be inaccurate yet the child may be sure that their reasoning works! They may use a phrase like, ' I reckon' and appear very confident!
And what of proof? What would it mean to prove that the solution was indeed the solution? There's the issue of checking back to see if the solution satisfies all the criteria - in this case that the two numbers suggested in each envelope do indeed add up to the number on the envelope and that we have not used any number more than once, as stated in the question. This element is emergent in the children's solutions above. For example, Ieuan talks about not using 4 + 4 because you can't use the same number twice. Rebekah notes that the total of each pair of numbers is what the envelope says. Would this constitute proof? In the case of this task that needs a specific solution we believe it would. However, other tasks may require other types of proof such as proof by exhaustion, proof by counter-example, proof by logical argument, proof by contradiction or generic proof. To find out more about these you may like to read our articles Mastering Mathematics: the Challenge of Generalising and Proof and Take One Example, which focuses on generic proof.
So, having explored a possible progression in reasoning how would you place Ellie on the spectrum of becoming expert at reasoning and what next steps would you offer her?

For my second solution, I tried a different solution for 14 which was 8 and 6. Then for 13 I had to use 9 and 4. There were two solutions to make 8 and this time I chose 5 and 3. Then 7 was made from 0 and 7 and 3 from 1 and 2 which all worked.
For my last solution, I used 8 and 6 for 14 again and 9 and 4 for 13. For 8, I used 7 and 1 which was different. To make 7, I used 5 and 2 (also different) and for 3, I used 0 and 3.
There were no other ways of making 14 so I knew I had found all the solutions.
So the numbers which could be inside the 8 envelope were 0 & 8, 5 & 3 or 7 & 1.
We would be delighted to receive examples of your learners' progression in reasoning as they tackle the Sealed Solution task. Do email us with their solutions and your commentary.
Here are some further examples from NRICH solutions that help us develop our thinking on reasoning.
Let's look at the task Make 37:
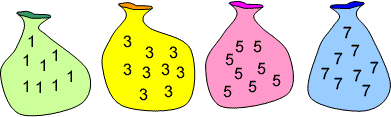
Pick any ten numbers from the bags above so that their total is 37.
Here is one of the solutions we received:
36 (10 numbers): 5 + 5 + 5 + 5 + 5 + 3 + 3 + 3 + 1 + 1
38 (10 numbers): 1 + 1 + 1 + 3 + 3 + 5 + 5 + 5 + 7 + 7
37 (9 numbers): 5 + 5 + 5 + 5 + 5 + 5 + 5 + 1 + 1
Here the child is moving into proof by showing that you cannot make an odd number with an even number of odd numbers. They are using mathematical generalisation. However, the chain of argument could be developed to show exactly why this can't work by showing why you can't make an odd number with an even number of odd numbers. Specific examples can be helpful for illustrative purposes yet they
do not constitute a watertight proof. This is a key development in reasoning with children and we need to model for them how to move beyond specific numerical examples to a general proof that holds good for all examples. So, this chain of reasoning needs to show that two odd numbers always make an even and that ten odd numbers is made up of five pairs of odd numbers. Therefore, there will be a
sum of five even numbers, which must be even.
What do you think of the chain of reasoning in this other solution to the same problem, Make 37? Has the child shown a complete chain of reasoning? Sometimes we can be glad that a child has given a reason at all. Sometimes it may be appropriate to challenge them further to provide a complete chain of reasoning. How true is this of your classroom? Is this a useful development
for you?
In addition, why not tackle one or more of these NRICH tasks which particularly lend themselves to developing reasoning:
Poly Plug Rectangles
Largest Even
Two Numbers Under the Microscope
Which Scripts?
Rectangle Tangle
Fraction Fascination
Looking at the children's solutions to the above offer some good examples of different stages of reasoning. In Largest Even, the first three solutions clearly describe what to do in order to solve the challenge, but they give no insight into how they arrived at these instructions. It is obvious that a lot of reasoning must have taken place, but the children have not communicated it. By contrast, learners at Kororoit Creek Primary School have moved beyond description into explanation. This is evident from the sentence structures they use, for example, "We could not make 99 because we only have one 9" (see below for more information about sentence structure). However, in Rectangle Tangle, Sophia demonstrates that an explanation does not necessarily need full sentences - she has annotated the image very effectively, using key words and phrases.
In responding to Two Numbers Under the Microscope, Peter has written a convincing solution and is beginning to justify his answer. He is developing a logical chain of reasoning, but he has missed out a few steps along the way. For example, it is not clear how he knows that two even numbers add together to make an even number. As Peter is focused on a general case rather than specific examples of odd numbers, he is almost at the stage of proof. In answering the same task, Amrit has used algebra to express an odd number and his solution offers a complete chain of reasoning, making it an algebraic proof.
Communicating reasoning
We now turn our attention to the other aspect of reasoning - that of communicating reasoning in a succinct, elegant and mathematical way. Here strategies that we use in Literacy will prove helpful to us in developing this mathematical communication with children. It is helpful to model the communication ourselves (both as articulating our own thought processes and also staging conversations with other adults in the room), give sentence starters to help children construct their argument and also give time in lessons to improving children's expression of their reasoning processes. Children need to understand how to refine their sentences and chains of reasoning, and how to use appropriate mathematical language. A working wall is a great place for examples of superb reasoning that children can refer to when improving their own chain of reasoning to become more succinct and elegant. They also could collect good examples in the back of their mathematics books with annotations to explain what makes them 'good'.
Here are some possible sentence starters:
- I think this because ...
- If this is true then ...
- I know that the next one is ... because ...
- This can't work because ...
- When I tried xxxx I noticed that ...
- The pattern looks like ...
- All the numbers begin with ...
- Because xxxx then I think xxxx
- This won't work because ...
You might want to develop a checklist for children to use when considering their reasoning communication or that of others. It will need to be age/development/knowledge appropriate. We suggest it could contain the following:
- How clear is the reasoning? Can I follow the argument?
- How logical is the reasoning? Does it form a chain of reasoning? Is it a complete or partial chain?
- Does the argument/explanation use reasoning language, such as 'because'?
- How succinct is the reasoning? Are the sentences short and to the point?
Let's look at some examples of NRICH solutions to see how well they fit these criteria. Let's look at Ieuan's solution to Sealed Solution again and this time, look at the communication of the reasoning. How do you think Ieuan is doing on the journey to becoming an expert communicator of reasoning using the criteria we offered above?
First, a brief reminder of the problem:
And now, Ieuan's solution again:
0 + 7=7 5 + 3=8 9 + 4 =13 6 + 8=14 2 + 1=3.
And then I tried using a system from then on, of adding a number to the smaller number then subtracting one from the smaller number, but it did not go very well because when I converted 5 + 3 to 4 + 4 I realised that you cannot do that.
Then I found out something quite clever that from one onward: each 2 numbers have the same amount of possibilities (I think by this Ieuan means that pairs of consecutive numbers have the same number of possibilities). For example 2 and 3 have two possibilities, 4 and 5 have have three, 6 and 7 have four, 8 and 9 have five and it goes on forever! So I wrote down all the possibilities for 7, 8, 13, 14, 3.
Then I shortened it, so if I use 13 as an example: 13+0, 12+1, 10+3, 9+4, 8+5, 7+6. Then I would take off 13+0, 12+1 and 10+3 and do that for all the rest! So when I had all the possibilities I did two attempts without succeding then I got one and I started explaining it on here, but I realised I had found the same as my first attempt.
Then I did one attempt and I found another: 3+0, 8+6, 9+4, 7+1 and 2+5.
It may be helpful to introduce the children to tables as a way of expressing their results and to support some clear reasoning. However, taker a look at the example below and see how much you think the chart helps with communicating the reasoning. It is not automatic that such 'organisational' tools promote a greater level of communication of reasoning. They may however help children who think in a certain way and they may help some children to find the solution.
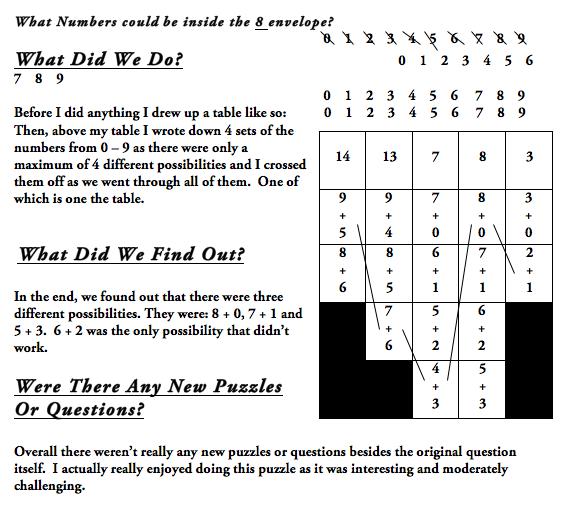
In this solution to the NRICH problem Heads and Feet we see some great use of a table to help with succinct communication yet the chain of reasoning needs further development. As stated earlier, we are often happy with some reasoning - we need to work with children to support them to develop complete chains of reasoning by encouraging more critical assessment of reasoning explanations. Here is the Heads and Feet task:


On a farm there were some hens and sheep.
Altogether there were 8 heads and 22 feet.
How many hens were there?
And here is the solution we are referring to:
I did trial and error to solve this problem:
Sheep feet: hen feet: heads: total feet
________________________________________________
4 : 2 : 2 : 6
8 : 4 : 4 : 12
12 : 6 : 6 : 18
The next line can't be one more sheep and one more hen or else there would be 24 feet instead of 22 feet, and there HAS to be two more heads/animals, so it ends up with two more hens.
In addition to 'organisational' tools the development of visual methods of proof, such as diagrams, may be helpful to explain reasoning. Particularly at primary level, visual proofs can be very useful as way to express a reasoned argument.
Beyond that we will want to offer children the opportunity to understand algebraic concepts and notation to help them express their reasoning in a succinct and elegant manner. Take a look at these two solutions to Eggs in Baskets and see whether you think the algebra has helped achieve this:
 There are three baskets, a brown one, a red one and a pink one, holding a total of ten eggs.
There are three baskets, a brown one, a red one and a pink one, holding a total of ten eggs.The Brown basket has one more egg in it than the Red basket.
The Red basket has three eggs less than the Pink basket.
How many eggs are in each basket?
Solution 1:
If there was 1 egg in the brown basket, no eggs in the red basket and 3 eggs in the pink basket, that would only make 4 eggs.
If there were 2 eggs in the brown basket, 1 egg in the red basket and 4 eggs in the pink basket, this only makes 7 eggs.
So finally, if there were 3 eggs in the brown basket, 2 eggs in the red basket and 5 eggs in the pink basket, there would be 10 eggs altogether.
In the 'words' version the child is showing evidence of moving towards becoming an expert communicator of reasoning. Their argument has a system to it - they try one egg in the brown basket and see what happens, then two eggs and then three. They are using the problem-solving skill of trial and improvement and systematically trying out different numbers of eggs. They are able to express their
thinking in a clear, succinct and logical way. Each sentence is compact and uses logical argument words such as 'if there were ”¦ there would be' and 'so finally'.
Here's the algebraic version. How does it help develop the communication? To what extent has it 'translated' the words in the first solution into mathematical symbols?
Red basket = n eggs
Brown basket = n+1 eggs
Pink basket = n+3 eggs
Total eggs = 10, so
n + (n+1) + (n+3) = 10
3n + 4 = 10
3n = 6
n = 2
So, brown basket - 3eggs
red basket - 2 eggs
pink basket - 5 eggs
Supporting children to move forwards with reasoning
Let's take a look at two children's solutions to Shape Times Shape:
Can you work out what they are from the multiplications below?
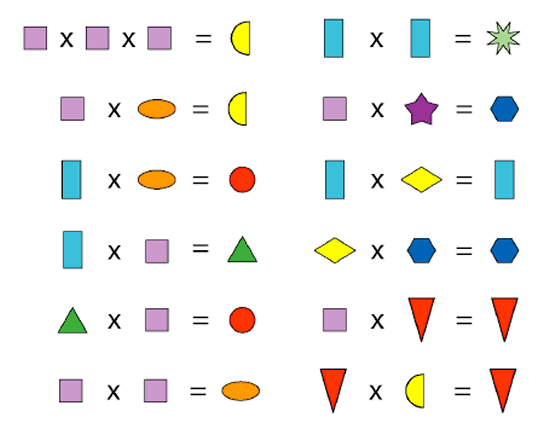
I worked out the purple square had to be two because three times three equals nine and nine times three equals twenty-seven which you can't do because the number has to be less than twelve and you can't do one because no two shapes can be the same number but two times two is four and four times two is eight.
Then I filled out the yellow semi circles as eight and the purple squares as two.
Then I worked out the second one down using what I already knew. Two times four is eight so I filled out all the orange ovals as four.
Then I worked out the red triangle equaled zero because only zero can times by a number and equal zero. Then I filled out all of the red triangles as zero.
Next I worked out the blue rectangles were three because one times one equals one which you can't do; I'd used two and four times four is sixteen which you also can't do so three times three is nine so the green star is nine. Then I filled out all the blue rectangles as three.
Then I worked out three times two equals six so I filled out all the green triangles as six.
Next I worked out six times two is twelve so I filled out all the red circles as twelve.
After I worked out three times one is three so the yellow diamond is one. Next I filled out all the yellow diamonds as one.
Next I looked at yellow diamond (one) times blue hexagon equals blue hexagon, and purple square (two) times purple star equals blue hexagon and thought nothing times two can equal seven so it had to be ten.
Finally I filled out all the blue hexagons as ten and the purple star as five seeing as two times five is ten.

It is interesting to consider how the two examples contrast - Lucy has used lot of words and the other child has used a more diagrammatical approach. Which do you think communicates more clearly? Do the diagrams help the clarity of the argument?
Secondly we may want to look at Lucy's explanation and think about whether it is her reasoning or her communication that we need to help her develop next. This is a key question that we need to be working on in the classroom. To what extent is it the actual reasoning or the communication of that reasoning that needs developing?
Conclusion
This article has looked at how developing excellence in reasoning with young learners is a complex matter. We need to think about the reasoning itself and understand the progression in that, as well as think about how we are going to support children to develop the communication of their reasoning. We need to value and promote reasoning explicitly, persistently, consistently and frequently and, in particular, help children to develop complete chains of reasoning. This aspect of mathematics will help us to deepen and extend our higher attainers as we take them onto generalisations and proof, whilst focusing on the same mathematical content.
We'd love to hear about your experiences of promoting reasoning. Do email us and do use the NRICH examples we have highlighted in this feature and encourage the children to send in examples of their reasoning. Enjoy!
Here is a PDF version of this article.

