Skip over navigation
Understanding the underlying structures of mathematics is fundamental to mastering the subject. This involves being fluent at generalising and proving. In this article, we look at what we mean by generalisation and proof, and how we can help learners get better at generalising and proving.
The problem-solving process
The problem-solving process can usually be thought of as having four stages, listed below along with the skills and strategies usually drawn upon during each stage:
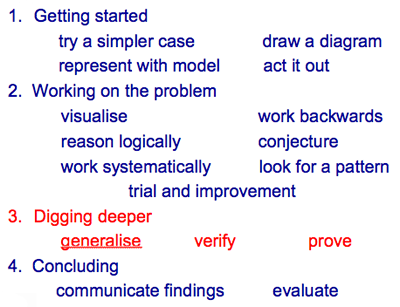
We can helpfully spend time with learners concentrating on each of these stages explicitly, in turn, as they learn to become confident problem solvers.
The third stage, 'Digging deeper' (in red above), takes place once the problem has been thoroughly explored and some solutions may have been found. Learners can be challenged to dig deeper by finding generalisations or a proof. NRICH believes that proof is the final step on the reasoning journey for youngsters as they progress from novice to expert. In our article Reasoning: The Journey from Novice to Expert, (part of our Reasoning Feature), we outline what NRICH sees as a five-step progression in reasoning; we look at examples using solutions to NRICH tasks and we discuss ways to help learners get better at communicating their reasoning.
But how can we help learners get better, in particular, at generalising and, ultimately, at proving?
Transferring thinking
Often the starting point of a task involves playing around with a particular example. Having worked on one specific example, a key skill in moving towards generalisation is to be able to transfer what you have learnt in that one example to another, new example. Similarities and differences between the two cases may become apparent. Exploring further examples means that strategies might emerge which always work, which is the essence of a generalisation (see below).
The idea of transferring thinking is one that we can work on with even quite young children. Secret Number is a lovely lower primary task which uses a calculator to explore the inverse relationship between addition and subtraction. You enter a 'secret
number' into the calculator, then ask a child what they would like to add to it. You enter '+' and then their chosen number and press '='. You show the child the result on the calculator and invite them to find out your secret number. Giving children time to explore this task in pairs and discussing how they worked out the secret number is a wonderful opportunity for learners to
transfer thinking. In this case, they might transfer a particular method, or methods, for finding the secret number.
Dotty Six, a dice game for young children, is also an engaging context in which to encourage learners to transfer thinking. In this case, learners might make more strategic choices in the way they play by transferring experiences from one game to the next. Two-digit
Targets offers similar opportunities as, when asked to compare their five numbers with another pair's and decide whose are 'better', learners may transfer some of their original thinking as they try to tweak their numbers to make them even better still!
Upper primary learners will enjoy getting stuck into Curious Number, which is structured so that learners tackle challenges with the same structure but which gradually increase in complexity. In this case, there are two elements to the transfer of thinking - transferring knowledge of divisibility rules and transferring a method of working systematically. (Of course, it's important to remember that learners are striving for a system, there is so such thing as the system. Be prepared to suspend your own way of approaching a task and to respect the varying systems which your learners will use!)
Display Boards also encourages transferring of thinking, this time in a spatial context. At the basic level, the series of challenges in this task help learners fully immerse themselves in the 'rules' so that mistakes made in the first part can be useful later. Display Boards also offers opportunities for transferring thinking in terms of a 'good' way of recording.
Dice in a Corner is another context in which you can transfer thinking from smaller to larger numbers of dice. This is a fascinating task in which, as yet, no generalisations have been found. Is there a generality? Can it be proven that there is no generalisation? We do not know the answer to this!
We have gathered together the tasks outlined above, which we feel offer opportunities for learners to transfer their thinking, here.
Generalising - seeing the underlying structure
During stage 2 of the problem-solving process ('Working on the problem'), children will be drawing on a number of key problem-solving skills (see the image of the whole process above). Looking for a pattern, in particular, will help them with the generalising process. For example, if a problem has generated a series of numbers such as:
2, 4, 6, 8 ...
Pattern-spotting will help them see the 'add two' pattern.
In addition, being able to transfer thinking will help learners generalise. Having transferred our thinking from one example to another, to another, to another ..., the emerging similarities and differences offer us insight into what will always be true in that situation, which in turn can be explained by its underlying mathematical structure. In short, being able to generalise a situation involves identifying its underlying mathematical structure.
Many tasks on the NRICH site have been designed to encourage primary learners to generalise. In Round the Two Dice learners roll a dice twice and make two two-digit numbers from the results. (For example rolling 2 and 4 would give 24 and 42.) The idea is to round each number to
the nearest 10 and the challenge is to find out whether both of the numbers ever round to the same multiple of 10. Learners might approach this task by trying lots of examples, transferring their thinking as they progress and then noticing similarities and differences between different rolls, leading to a generalisation.
The task Lots of Lollies focuses on multiples of 2 and 5 and provides a very accessible context in which transferring thinking can progress to generalisation. The beauty of this task is that the generalisation can be expressed in a number of different ways.
The nim family of games is a good source of generalisation too. Learners can start with Nim-7, which involves just seven counters and then progress to Stop the Clock and Got It. In each case, the game offers opportunities to generalise the
strategy for winning when the game is tweaked, for example by having more counters in Nim-7, or by changing the target number in Got It. If learners have chance to play Stop the Clock or Got It after trying Nim-7, you can observe whether they realise that the underlying structure of all three
games is identical ('isomorphic').
Six Numbered Cubes is a great context in which to develop learners' abiility to generalise. In this case, the generalisation is rooted in the way in which a cube's position affects how many of its faces are visible and therefore the possible total. If learners are looking for a high total, where should the '6 cube' go? Where should the '1 cube' go?
Button-up Some More, also offers several avenues for generalisation. For example, for four buttons, learners might articulate the fact that the position of the starting button doesn't matter - if I find six ways to button up my coat starting with the first button, there will be six ways starting with the second button, six with the third and six with the fourth. No matter which button you start with, there are always three other buttons left to do up and their positions are irrelevant. Other learners might notice that the total number of ways of doing up a coat can be found by multiplying the number of buttons it has by the number of ways you can do it up with one fewer button.
We have gathered together the tasks outlined above, which we feel offer opportunities for generalising, here.
Proving
Proving takes learners beyond conjecturing (stage 2 of the problem-solving process) and generalising (stage 3) to being able to construct a 'complete and convincing argument to support the truth of an assertion, which proceeds logically from the assumptions to the conclusion' (Haylock, 2006). This is an essential element of mastering mathematics.
As well as being part of the problem-solving process, we suggest that being able to prove is also the highest step on the reasoning journey (see our Reasoning Feature and particularly our article Reasoning: the Journey from Novice to Expert), following on from convincing and justifying. I may be convinced that a solution is correct, but I might simply have omitted a possibility or my mathematical argument may be incorrect. I might be able to justify my solution, which would involve some logical reasoning, but the key to proof is being able to articulate a watertight argument. For proof to be accessible to all primary children we need to use a strategy for communicating proof that isn't dependent on an understanding of complex abstract symbols or algebraic thinking. This is where visual proof can be useful.
Modes of communicating proof
There are three main ways to communicate a proof: visually, algebraically and by making a series of statements. All three are underpinned by logical reasoning.
Square Subtraction is a useful task in which to consider both visual and algebraic proofs. Here is the task:
In this case, a dot pattern provides the basis of a visual proof. Here is an image to show my chosen starting number, 6, squared. I then take away that starting number, 6, from the diagonal (shown with a green line):
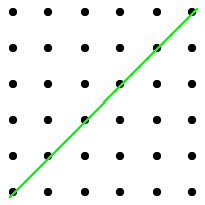
Can you see why this will always leave an even number?
Perhaps you noticed that the diagonal is a line of symmetry so that the number of dots on one side is equal to the number of dots on the other. This means we have 'two lots of' the same number of dots. We know that any multiple of 2 is an even number, so the total number of dots left after the diagonal is removed is even. Any number squared can be represented by a square array, so this reasoning will be true whether the starting number is odd or even.
To support learners in their understanding and use of visual proof, it might be fruitful to present them with an example of an image used in a visual proof, such as the one above for Square Subtraction, and ask them to tell the story of the image, rather than expecting them to create their own visual proofs from scratch at first. Although an image or diagram is the focal part of a visual proof, additional text will always be needed to complete the proof.
How would you create an algebraic proof for the same challenge, Square Subtraction?
We received the following solution to Square Subtraction from Victor and Elliot who go to Kenakena SchoolӬ in New Zealand:
Victor and Elliot use algebra to represent odd and even numbers and are able to prove that the result will always be even, as in both cases the answer is a multiple of 2. They are perhaps not completely fluent with this tool yet, as they have not quite developed the associated vocabulary, but they appear to have grasped the crucial elements of expressing numbers using symbols, and manipulating them.
Six Ten Total is another good example of a task which lends itself to both visual and algebraic proof for upper primary. Do take a look at it and see what you think.
The cooperative challenge in Strike It Out gives even younger learners the chance to prove using a series of statements. You can start by inviting them to prove it is possible to create a string of number sentences that uses all the numbers on the 0-20 number line.
A proof might look like this:
If zero is included in the number sentence then all three numbers are not distinct.
This is true whether you use addition or subtraction in your number sentence.
This does not obey the rules of the game.
Therefore, on a 0-20 number line we cannot ever use up all the numbers.
Methods for proving
At primary level, we find it helpful to consider five different methods we can use for proving, each of which might lend themselves to visual, algebraic and/or written modes of communication:
Proof by exhaustion
You may well have come across this before in the context of 'finding all possibilities'. In order to create a proof by exhaustion, learners need to have a systematic way of working to exhaustively list all the possible outcomes. Our Working Systematically Feature includes this set of tasks, all of which focus on finding all solutions.
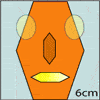At lower primary, Robot Monsters, is particularly appealing to some learners as they are asked to create all the different possible monsters from the given head, body and leg parts. 6 Beads is another accessible example in which learners are finding all the possible
ways to arrange six beads on a ones and tens abacus. School Fair Necklaces is also an example of a challenge in which the total number of possible solutions is relatively small, so that learners can prove that all the possibilities have been found. (The teachers' resources sections of both School Fair Necklaces and 6 Beads outline a way to help learners understand what is meant by 'working systematically'.)
At upper primary, the following tasks all offer opportunities for proof by exhaustion as part of their solution: The Dice Train, Sealed Solution, Factor Lines and Reach 100.
Proof by counter example
Five Steps to 50 is a task which lends itself to the progression from transferring thinking to generalising and on to proof by counter example. Learners throw a dice twice to make a two-digit starting number and then they must make exactly five steps of either 1, 10 or 100 to get to 50 exactly. As they try lots of examples, learners might start to collect a list of starting numbers which do work and those which don't. They will notice patterns and someone might make a conjecture, such as "I think that all the numbers which have the same tens and ones digit work". Quite often, another learner will quickly refute this conjecture by presenting a counter example, in other words a number which does have the same tens digit as ones digit, but that doesn't work.
Proof by contradiction
Play to 37 focuses on the structure of odd and even numbers and exploring the conjecture "I need to go second in order to win" provides an opportunity for constructing proof by contradiction. In fact, it also lends itself to visual or algebraic proof. (The numbers used could easily be adapted so that the arithmetic becomes less onerous.) Why don't you take a look? Can you use a visual proof to solve this problem?
Proof by logical reasoning
The series of statements referred to above in the context of Strike It Out is a good example of proof by logical reasoning. The key to a proof by logical reasoning is to include every single step in the reasoning process, leaving nothing unexplained. Learners can be challenged further to prove whether it is possible to create a string of number sentences that uses all the numbers on the 1-20 number line. What about on any number line with a set of consecutive whole numbers?
Two of the tasks we originally wrote for the Young Mathematicians' Award offer opportunities to prove by logical reasoning. In Six Ten Total, one of the things learners may notice is that the total of the dice is always a multiple of 4 and the challenge explicitly asks them to try to prove anything they have noticed. There are both algebraic and visual ways of doing this. In Six Numbered Cubes, learners are required to prove by logical reasoning that, if the cubes are arranged in a vertical tower, then whatever the order of the cubes, you cannot produce a total of 80.
Generic proof
In generic proof, a carefully selected example helps you to see, in that one example, the underlying general structure. Two Numbers Under the Microscope is an example of generic proof (as is Square Subtraction already discussed above). Learners are asked to choose two odd numbers and find their total. They are invited to make a model of their numbers and then they are shown these pictures/models made by others:
The idea is for learners to look closely at the models and picture, and to articulate whether they can see anything in any of them that would work in exactly the same way if two different odd numbers were used.
Take Three Numbers, Three Neighbours and Odd Times Even are all good contexts in which to explore generic proof further (and all three of these tasks lend themselves to a visual mode of communication too). You may also find the article Take One Example useful on the subject of generic proof.
We have gathered together the tasks outlined above, which we feel offer opportunities for learners to prove, here.
In conclusion
Taking the problem-solving process into generalisation and proof is challenging. Children will need repeated opportunities to focus on this third stage and will benefit from the chance to discuss what it entails regularly. They will need practice both with the five different methods for proving and the modes of communicating these. In becoming fluent with proof, they are also becoming experts at reasoning and all this will contribute towards their mastering of mathematics.
Finally, why not have a go at Dicey Addition and/or Dicey Operations in Line with your class once you have worked on generalisation and proof with them? We feel that these two tasks are wonderful examples of contexts in which learners could demonstrate the progression from transferring thinking to generalising and on to proof by exhaustion combined with proof by logical reasoning! Do let us know how you get on.
This article and feature are part of a series. You may also find the following features of interest in relation to generalising and proof:
Problem Solving
Reasoning
References
Haylock, D. (2006) Maths explained for primary teachers. London, Sage.
Further reading
You may like to read Andreas Stylianides' article Breaking the Equation 'Empirical Argument = Proof'. Set in a secondary context, it discusses how we can help learners understand the limitations of empirical arguments.
Here is a PDF version of this article.
Mastering Mathematics: the Challenge of Generalising and Proof
Understanding the underlying structures of mathematics is fundamental to mastering the subject. This involves being fluent at generalising and proving. In this article, we look at what we mean by generalisation and proof, and how we can help learners get better at generalising and proving.
The problem-solving process
The problem-solving process can usually be thought of as having four stages, listed below along with the skills and strategies usually drawn upon during each stage:
We can helpfully spend time with learners concentrating on each of these stages explicitly, in turn, as they learn to become confident problem solvers.
The third stage, 'Digging deeper' (in red above), takes place once the problem has been thoroughly explored and some solutions may have been found. Learners can be challenged to dig deeper by finding generalisations or a proof. NRICH believes that proof is the final step on the reasoning journey for youngsters as they progress from novice to expert. In our article Reasoning: The Journey from Novice to Expert, (part of our Reasoning Feature), we outline what NRICH sees as a five-step progression in reasoning; we look at examples using solutions to NRICH tasks and we discuss ways to help learners get better at communicating their reasoning.
But how can we help learners get better, in particular, at generalising and, ultimately, at proving?
Transferring thinking
Often the starting point of a task involves playing around with a particular example. Having worked on one specific example, a key skill in moving towards generalisation is to be able to transfer what you have learnt in that one example to another, new example. Similarities and differences between the two cases may become apparent. Exploring further examples means that strategies might emerge which always work, which is the essence of a generalisation (see below).
The idea of transferring thinking is one that we can work on with even quite young children. Secret Number is a lovely lower primary task which uses a calculator to explore the inverse relationship between addition and subtraction. You enter a 'secret
number' into the calculator, then ask a child what they would like to add to it. You enter '+' and then their chosen number and press '='. You show the child the result on the calculator and invite them to find out your secret number. Giving children time to explore this task in pairs and discussing how they worked out the secret number is a wonderful opportunity for learners to
transfer thinking. In this case, they might transfer a particular method, or methods, for finding the secret number. Dotty Six, a dice game for young children, is also an engaging context in which to encourage learners to transfer thinking. In this case, learners might make more strategic choices in the way they play by transferring experiences from one game to the next. Two-digit
Targets offers similar opportunities as, when asked to compare their five numbers with another pair's and decide whose are 'better', learners may transfer some of their original thinking as they try to tweak their numbers to make them even better still!Upper primary learners will enjoy getting stuck into Curious Number, which is structured so that learners tackle challenges with the same structure but which gradually increase in complexity. In this case, there are two elements to the transfer of thinking - transferring knowledge of divisibility rules and transferring a method of working systematically. (Of course, it's important to remember that learners are striving for a system, there is so such thing as the system. Be prepared to suspend your own way of approaching a task and to respect the varying systems which your learners will use!)
Display Boards also encourages transferring of thinking, this time in a spatial context. At the basic level, the series of challenges in this task help learners fully immerse themselves in the 'rules' so that mistakes made in the first part can be useful later. Display Boards also offers opportunities for transferring thinking in terms of a 'good' way of recording. Dice in a Corner is another context in which you can transfer thinking from smaller to larger numbers of dice. This is a fascinating task in which, as yet, no generalisations have been found. Is there a generality? Can it be proven that there is no generalisation? We do not know the answer to this!
We have gathered together the tasks outlined above, which we feel offer opportunities for learners to transfer their thinking, here.
Generalising - seeing the underlying structure
During stage 2 of the problem-solving process ('Working on the problem'), children will be drawing on a number of key problem-solving skills (see the image of the whole process above). Looking for a pattern, in particular, will help them with the generalising process. For example, if a problem has generated a series of numbers such as:
2, 4, 6, 8 ...
Pattern-spotting will help them see the 'add two' pattern.
In addition, being able to transfer thinking will help learners generalise. Having transferred our thinking from one example to another, to another, to another ..., the emerging similarities and differences offer us insight into what will always be true in that situation, which in turn can be explained by its underlying mathematical structure. In short, being able to generalise a situation involves identifying its underlying mathematical structure.
Many tasks on the NRICH site have been designed to encourage primary learners to generalise. In Round the Two Dice learners roll a dice twice and make two two-digit numbers from the results. (For example rolling 2 and 4 would give 24 and 42.) The idea is to round each number to
the nearest 10 and the challenge is to find out whether both of the numbers ever round to the same multiple of 10. Learners might approach this task by trying lots of examples, transferring their thinking as they progress and then noticing similarities and differences between different rolls, leading to a generalisation.The task Lots of Lollies focuses on multiples of 2 and 5 and provides a very accessible context in which transferring thinking can progress to generalisation. The beauty of this task is that the generalisation can be expressed in a number of different ways.
The nim family of games is a good source of generalisation too. Learners can start with Nim-7, which involves just seven counters and then progress to Stop the Clock and Got It. In each case, the game offers opportunities to generalise the
strategy for winning when the game is tweaked, for example by having more counters in Nim-7, or by changing the target number in Got It. If learners have chance to play Stop the Clock or Got It after trying Nim-7, you can observe whether they realise that the underlying structure of all three
games is identical ('isomorphic').Six Numbered Cubes is a great context in which to develop learners' abiility to generalise. In this case, the generalisation is rooted in the way in which a cube's position affects how many of its faces are visible and therefore the possible total. If learners are looking for a high total, where should the '6 cube' go? Where should the '1 cube' go?
Button-up Some More, also offers several avenues for generalisation. For example, for four buttons, learners might articulate the fact that the position of the starting button doesn't matter - if I find six ways to button up my coat starting with the first button, there will be six ways starting with the second button, six with the third and six with the fourth. No matter which button you start with, there are always three other buttons left to do up and their positions are irrelevant. Other learners might notice that the total number of ways of doing up a coat can be found by multiplying the number of buttons it has by the number of ways you can do it up with one fewer button.
We have gathered together the tasks outlined above, which we feel offer opportunities for generalising, here.
Proving
Proving takes learners beyond conjecturing (stage 2 of the problem-solving process) and generalising (stage 3) to being able to construct a 'complete and convincing argument to support the truth of an assertion, which proceeds logically from the assumptions to the conclusion' (Haylock, 2006). This is an essential element of mastering mathematics.
As well as being part of the problem-solving process, we suggest that being able to prove is also the highest step on the reasoning journey (see our Reasoning Feature and particularly our article Reasoning: the Journey from Novice to Expert), following on from convincing and justifying. I may be convinced that a solution is correct, but I might simply have omitted a possibility or my mathematical argument may be incorrect. I might be able to justify my solution, which would involve some logical reasoning, but the key to proof is being able to articulate a watertight argument. For proof to be accessible to all primary children we need to use a strategy for communicating proof that isn't dependent on an understanding of complex abstract symbols or algebraic thinking. This is where visual proof can be useful.
Modes of communicating proof
There are three main ways to communicate a proof: visually, algebraically and by making a series of statements. All three are underpinned by logical reasoning.
Square Subtraction is a useful task in which to consider both visual and algebraic proofs. Here is the task:
Choose any number. This is going to be your particular number for this proof.
Square your chosen number.
Subtract your starting number.
Is the number you're left with odd or even?
Create a model or a picture of your calculation, using your chosen number, and examine this model carefully.
Can you use this one model to prove that your result is always true and not just true for the particular number that you chose to start with?
Square your chosen number.
Subtract your starting number.
Is the number you're left with odd or even?
Create a model or a picture of your calculation, using your chosen number, and examine this model carefully.
Can you use this one model to prove that your result is always true and not just true for the particular number that you chose to start with?
In this case, a dot pattern provides the basis of a visual proof. Here is an image to show my chosen starting number, 6, squared. I then take away that starting number, 6, from the diagonal (shown with a green line):
Can you see why this will always leave an even number?
Perhaps you noticed that the diagonal is a line of symmetry so that the number of dots on one side is equal to the number of dots on the other. This means we have 'two lots of' the same number of dots. We know that any multiple of 2 is an even number, so the total number of dots left after the diagonal is removed is even. Any number squared can be represented by a square array, so this reasoning will be true whether the starting number is odd or even.
To support learners in their understanding and use of visual proof, it might be fruitful to present them with an example of an image used in a visual proof, such as the one above for Square Subtraction, and ask them to tell the story of the image, rather than expecting them to create their own visual proofs from scratch at first. Although an image or diagram is the focal part of a visual proof, additional text will always be needed to complete the proof.
How would you create an algebraic proof for the same challenge, Square Subtraction?
We received the following solution to Square Subtraction from Victor and Elliot who go to Kenakena SchoolӬ in New Zealand:
If n and e are arbitrary whole numbers, then even = $2n$ (I think by this they mean that you can write an even number as $2n$)
So even - even $= 2n - 2e = 2(n - e)$.
Thereby, even - even = even.
So odd$ = 2n + 1$
So odd - odd = $2n + 1 - (2e + 1) = 2n - 2e + 1 - 1 = 2(n- e)$.
Thereby, odd minus odd = even.
So even - even $= 2n - 2e = 2(n - e)$.
Thereby, even - even = even.
So odd$ = 2n + 1$
So odd - odd = $2n + 1 - (2e + 1) = 2n - 2e + 1 - 1 = 2(n- e)$.
Thereby, odd minus odd = even.
Victor and Elliot use algebra to represent odd and even numbers and are able to prove that the result will always be even, as in both cases the answer is a multiple of 2. They are perhaps not completely fluent with this tool yet, as they have not quite developed the associated vocabulary, but they appear to have grasped the crucial elements of expressing numbers using symbols, and manipulating them.
Six Ten Total is another good example of a task which lends itself to both visual and algebraic proof for upper primary. Do take a look at it and see what you think.
The cooperative challenge in Strike It Out gives even younger learners the chance to prove using a series of statements. You can start by inviting them to prove it is possible to create a string of number sentences that uses all the numbers on the 0-20 number line.
A proof might look like this:
If zero is included in the number sentence then all three numbers are not distinct.
This is true whether you use addition or subtraction in your number sentence.
This does not obey the rules of the game.
Therefore, on a 0-20 number line we cannot ever use up all the numbers.
Methods for proving
- Proof by exhaustion - this depends on there being a small number of results so that it is manageable to find all possibilities; it is about working systematically.
- Proof by counter example - an example that doesn't work disproves the conjucture.
- Proof by contradiction - we assume that what we want to prove is not true, and then show that the consequences of this are not possible.
- Proof by logical reasoning - the chain of reasoning is complete, with no room for ambiguity and no missing steps.
- Generic proof - a carefully selected example enables anyone to see, in that example, the general structure.
Proof by exhaustion
You may well have come across this before in the context of 'finding all possibilities'. In order to create a proof by exhaustion, learners need to have a systematic way of working to exhaustively list all the possible outcomes. Our Working Systematically Feature includes this set of tasks, all of which focus on finding all solutions.
At lower primary, Robot Monsters, is particularly appealing to some learners as they are asked to create all the different possible monsters from the given head, body and leg parts. 6 Beads is another accessible example in which learners are finding all the possible
ways to arrange six beads on a ones and tens abacus. School Fair Necklaces is also an example of a challenge in which the total number of possible solutions is relatively small, so that learners can prove that all the possibilities have been found. (The teachers' resources sections of both School Fair Necklaces and 6 Beads outline a way to help learners understand what is meant by 'working systematically'.) At upper primary, the following tasks all offer opportunities for proof by exhaustion as part of their solution: The Dice Train, Sealed Solution, Factor Lines and Reach 100.
Proof by counter example
Five Steps to 50 is a task which lends itself to the progression from transferring thinking to generalising and on to proof by counter example. Learners throw a dice twice to make a two-digit starting number and then they must make exactly five steps of either 1, 10 or 100 to get to 50 exactly. As they try lots of examples, learners might start to collect a list of starting numbers which do work and those which don't. They will notice patterns and someone might make a conjecture, such as "I think that all the numbers which have the same tens and ones digit work". Quite often, another learner will quickly refute this conjecture by presenting a counter example, in other words a number which does have the same tens digit as ones digit, but that doesn't work.
Proof by contradiction
Play to 37 focuses on the structure of odd and even numbers and exploring the conjecture "I need to go second in order to win" provides an opportunity for constructing proof by contradiction. In fact, it also lends itself to visual or algebraic proof. (The numbers used could easily be adapted so that the arithmetic becomes less onerous.) Why don't you take a look? Can you use a visual proof to solve this problem?
Proof by logical reasoning
The series of statements referred to above in the context of Strike It Out is a good example of proof by logical reasoning. The key to a proof by logical reasoning is to include every single step in the reasoning process, leaving nothing unexplained. Learners can be challenged further to prove whether it is possible to create a string of number sentences that uses all the numbers on the 1-20 number line. What about on any number line with a set of consecutive whole numbers?
Two of the tasks we originally wrote for the Young Mathematicians' Award offer opportunities to prove by logical reasoning. In Six Ten Total, one of the things learners may notice is that the total of the dice is always a multiple of 4 and the challenge explicitly asks them to try to prove anything they have noticed. There are both algebraic and visual ways of doing this. In Six Numbered Cubes, learners are required to prove by logical reasoning that, if the cubes are arranged in a vertical tower, then whatever the order of the cubes, you cannot produce a total of 80.
Generic proof
In generic proof, a carefully selected example helps you to see, in that one example, the underlying general structure. Two Numbers Under the Microscope is an example of generic proof (as is Square Subtraction already discussed above). Learners are asked to choose two odd numbers and find their total. They are invited to make a model of their numbers and then they are shown these pictures/models made by others:
Adam found some dominoes with 5 and 9 spots on them:
Sarai made a model using Multilink cubes:
Abdul drew a picture of 5 add 9 like this:
Sarai made a model using Multilink cubes:
Abdul drew a picture of 5 add 9 like this:
The idea is for learners to look closely at the models and picture, and to articulate whether they can see anything in any of them that would work in exactly the same way if two different odd numbers were used.
Take Three Numbers, Three Neighbours and Odd Times Even are all good contexts in which to explore generic proof further (and all three of these tasks lend themselves to a visual mode of communication too). You may also find the article Take One Example useful on the subject of generic proof.
We have gathered together the tasks outlined above, which we feel offer opportunities for learners to prove, here.
In conclusion
Taking the problem-solving process into generalisation and proof is challenging. Children will need repeated opportunities to focus on this third stage and will benefit from the chance to discuss what it entails regularly. They will need practice both with the five different methods for proving and the modes of communicating these. In becoming fluent with proof, they are also becoming experts at reasoning and all this will contribute towards their mastering of mathematics.
Finally, why not have a go at Dicey Addition and/or Dicey Operations in Line with your class once you have worked on generalisation and proof with them? We feel that these two tasks are wonderful examples of contexts in which learners could demonstrate the progression from transferring thinking to generalising and on to proof by exhaustion combined with proof by logical reasoning! Do let us know how you get on.
This article and feature are part of a series. You may also find the following features of interest in relation to generalising and proof:
Problem Solving
Reasoning
References
Haylock, D. (2006) Maths explained for primary teachers. London, Sage.
Further reading
You may like to read Andreas Stylianides' article Breaking the Equation 'Empirical Argument = Proof'. Set in a secondary context, it discusses how we can help learners understand the limitations of empirical arguments.
Here is a PDF version of this article.