Skip over navigation
Cubist Cuts
Age 11 to 14
Challenge Level 
Use cubes made from smaller cubes (e.g. multilink) to help you. For the 3x3x3 cube, think about "freeing" the centre unit cube.
You may also like
All in the Mind
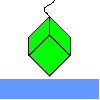
Imagine you are suspending a cube from one vertex and allowing it to hang freely. What shape does the surface of the water make around the cube?
Instant Insanity
Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?