Skip over navigation
Can you express $\overrightarrow{DC}$ in terms of $\bf{x}$ and $\bf{y}$?
Can you express $\overrightarrow{BE}$in terms of $\bf{x}$ and $\bf{y}$?
By writing $\overrightarrow{DG}$ as $\lambda \overrightarrow{DC}$ and $\overrightarrow{BG}$ as $\mu \overrightarrow{BE}$, can you find two expressions for $\overrightarrow{AG}$?
By equating coefficients of $\bf{x}$ and $\bf{y}$, can you find $\lambda$?
Now you can use this information together with the first two hints in the problem to find the relationships between the areas.
Another Triangle in a Triangle
Age 16 to 18
Challenge Level 
An alternative approach is to use vectors.
In the diagram below, vectors $\bf{x}$ and $\bf{y}$ have been defined such that $\overrightarrow{AC}=3\bf{x}$ and $\overrightarrow{AB}=3\bf{y}$.
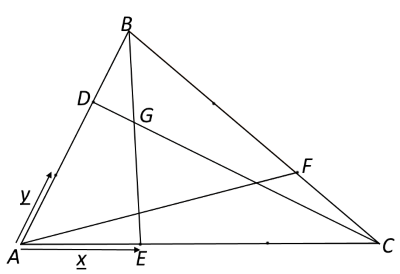
Click below for a series of hints to help you to work out the ratio of the length $DG$ to $DC$:
In the diagram below, vectors $\bf{x}$ and $\bf{y}$ have been defined such that $\overrightarrow{AC}=3\bf{x}$ and $\overrightarrow{AB}=3\bf{y}$.
Click below for a series of hints to help you to work out the ratio of the length $DG$ to $DC$:
Can you express $\overrightarrow{DC}$ in terms of $\bf{x}$ and $\bf{y}$?
Can you express $\overrightarrow{BE}$in terms of $\bf{x}$ and $\bf{y}$?
By writing $\overrightarrow{DG}$ as $\lambda \overrightarrow{DC}$ and $\overrightarrow{BG}$ as $\mu \overrightarrow{BE}$, can you find two expressions for $\overrightarrow{AG}$?
By equating coefficients of $\bf{x}$ and $\bf{y}$, can you find $\lambda$?
Now you can use this information together with the first two hints in the problem to find the relationships between the areas.
You may also like
Napoleon's Hat
Three equilateral triangles ABC, AYX and XZB are drawn with the point X a moveable point on AB. The points P, Q and R are the centres of the three triangles. What can you say about triangle PQR?
Plane to See
P is the midpoint of an edge of a cube and Q divides another edge in the ratio 1 to 4. Find the ratio of the volumes of the two pieces of the cube cut by a plane through PQ and a vertex.