Count Me In

Count Me In

Count Me In printable sheet
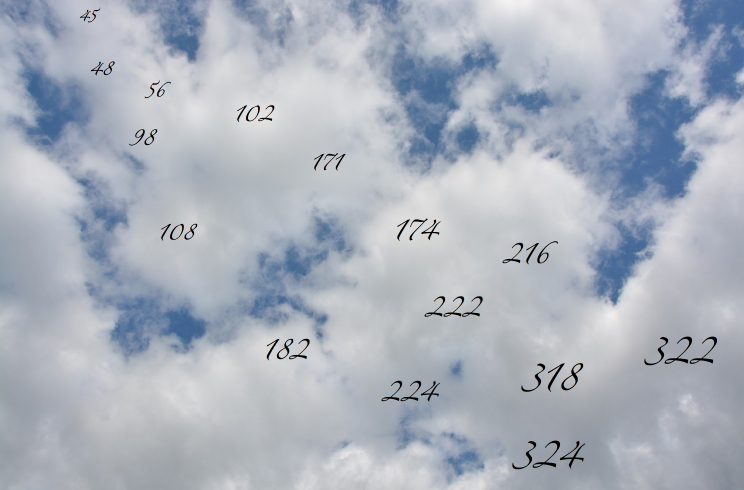
Which of these numbers would you come to when counting in sixes from zero?
How do you know?

Would you get to some of these numbers if you were counting in sevens from zero? Which ones?
Can you explain how you arrived at your answers?

Could some of these numbers be reached if you were counting in nines from zero? Which ones?
Again, how do you know?

Would your answers be the same if you counted in the same step sizes but down from 350 in each case?
How do you know?

 

Looking at the image above and this time counting in 25s from zero, which numbers will you land on?  
If you were counting in 25s from 10, which numbers would you land on this time?  How can you work this out without actually counting?
 

Why do this problem?

This activity gives pupils an opportunity to combine counting accurately with addition and their knowledge of multiples and factors.

Possible approach

You could introduce the task by doing some skip counting outloud as a whole group.  Your choice of starting number and step will depend on the children's experiences, but to begin with you might want to start at zero every time, as these challenges do.  Going up in twos, fives and tens would be good starting points. It is helpful to point out to learners that if they struggle to keep up, it does not matter as they can opt back in again at any time. It is interesting to note that when going up in twos, the silence 'contains' the missed-out numbers, but as the step size increases, learners may add rather than count as such.

In this context, you could invite learners to predict whether or not they will land on certain numbers, such as 25, 80 and 102, and how they know.  

You can then introduce the task as it is written and pairs or children could work together.  Encourage them to rehearse their reasoning so that if asked they could justify their answer to the whole group.

Key questions

How did you go about getting you answers?
Did you use the same methods for 6, 7, 9, and 25?
 

Possible extension

Challenge children to count back in different step sizes as well as up.
You could even split the class into two groups and invite one group to count, for example, from 1 up in threes and the second group to count, for example, from 102 down in fives.  Will the two groups ever say the same number at the same time?  (When trying challenges like this, suggest at first that the groups alternate counts so that learners' attention can be developed before building up to counting at exactly the same time.)
 

Possible support

A hundred square (perhaps even more than one copy) could be a useful tool for some children.