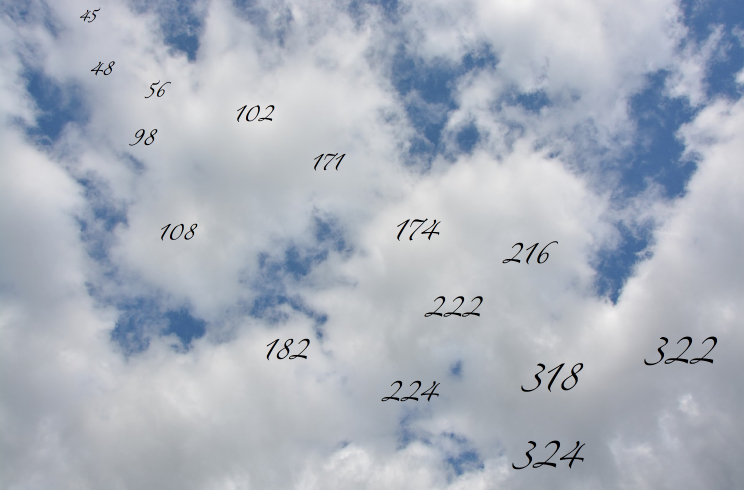Count Me In

Andy and Mr Morris' Maths Group sent in a very comprehensive solution to this challenge, thank you all! Here is the image for the first part of the problem:  

Here are the group's responses:

1. Which of these numbers would you come to when counting in sixes from zero?
   How do you know?
   1. If 2 and 3 are factors of 6, then multiples of 6 must be divisible by 2 and 3.
   2. If a number is a multiple of two, then it must be an even number and end in the digit 0, 2, 4, 6 or 8.
   3. To tell if a number is a multiple of three, you need to add all the individual digits up and see if the total is a multiple of three. If it is, then the number itself is a multiple of three.
   4. Take 108 for example, 1+0+8=9, 9 is a multiple of 3 so we know that 108 is a multiple of 3.
   5. Therefore, you would come across 102, 108, 174, 216, 222, 318 and 324.
       
2. Would you get to some of these numbers if you were counting in sevens from zero? Which ones? Can you explain how you arrived at your answers?
   1. Take the last digit of the number, double it then subtract from the number that the remaining digits make. If that number is divisible by 7, the original number is a multiple of seven.
   2. Take 224 for example, the last digit is 4 so if you double it you get 8. Then you subtract from the remaining number so 22-8=14. Finally, 14 is a multiple of 7, so 224 is a multiple of 7!
   3. Using this method, we can work out that we would get to the following numbers: 224 and 322. I wonder whether you have missed a couple of the smaller numbers out here...
       
3. Could some of these numbers be reached if you were counting in nines from zero? Which ones? Again, how do you know?
   1. The numbers would be reached if they are multiples of 9. To know if a number is a multiple of 9, you need to add the individual digits up, if they add up to a multiple of 9, then the original number is a multiple of 9.
   2. Take 324 for example, 3+2+4=9, 9 is a multiple of 9 so 324 is in the 9 times table and would be reached.
   3. Therefore, the numbers you would reach are 45, 108, 171, 216 and 324.
       
4. Would your answers be the same if you counted in the same step sizes but down from 350 in each case? How do you know? 
   1. Your answers would only stay the same if the step size is a factor of 350.
   2. You can tell if a number is a factor of 350 by using the same methods as before.
      1. 6 is not a factor of 350. I know this because although it is an even number and therefore a multiple of 2, it is not a multiple of 3. We know this because if you add the digits (3+5+0) you get 8 which is not a multiple of 3. So 350 is not divisible by 6 and your answers would not be the same.
      2. 7 is a factor of 350. 0 is the last digit so if you double it you get 0 again. 35-0=35. 35 is a multiple of 7, so 7 is a factor of 350. So 350 is divisible by 7 and your answers would be the same.
      3. 9 is not a factor of 350. I know this because 3+5+0=8 and 8 is not a multiple of 9. Therefore, 9 is not a factor of 350 and your answers would not be the same.
   3. So as 7 is a factor of 350, the answers would stay the same but as 6 and 9 are not factors of 350 the answers are not going to be the same.

What great reasoning all of you! I'm also intrigued to know whether you can explain why your divisibility test for 7 works...

Here is the second image in the problem:

Here are the group's solutions for the second part of the task:

1. Looking at the image above and this time counting in 25s from zero, which numbers will you land on?
   1. If a number is a multiple of 25, it must end in one of the following pairs of digits; 00, 25, 50 or 75.
   2. Therefore, if you count in 25s from 0, you would land on 175, 200, 350, 400, 650, 900 and 975.
       
2. If you were counting in 25s from 10, which numbers would you land on this time?  How can you work this out without actually counting?
   1. If you count in 25s from 10, you use the same rule as last question but must factor in the difference of 10. So if we add 10 to each of 00, 25, 50 or 75, we get 10, 35, 60 and 85 and therefore you would only land on numbers that end with one of the following pairs of digits 10, 35, 60 and 85.
   2. Therefore, if you count in 25s from 10, you would only land on 310 and 710.

Thank you to you all!