Skip over navigation
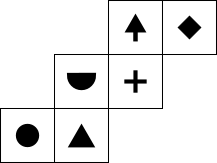The net on the right is folded into a cube.
It is placed on a table with the face
on top.
Which face is at the bottom?
This problem is taken from the World Mathematics Championships
Which Face?
Age 14 to 16
ShortChallenge Level 
The net on the right is folded into a cube.It is placed on a table with the face
on top.Which face is at the bottom?
This problem is taken from the World Mathematics Championships
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Nine Colours
Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?
The Spider and the Fly
A spider is sitting in the middle of one of the smallest walls in a room and a fly is resting beside the window. What is the shortest distance the spider would have to crawl to catch the fly?
Hamiltonian Cube
Weekly Problem 36 - 2007
Find the length along the shortest path passing through certain points on the cube.