Skip over navigation
Folding up the net
Imagine folding the net into a cube, starting with the face
, and continuing until it reaches the top.
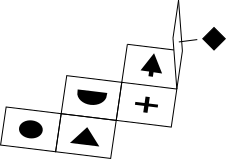
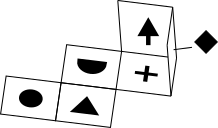
So the face
is at the bottom when the face is at the top.
Considering edges
Imagine the top and the base of a cube. The top shares a (green) edge with each side that isn't the base. The base shares a (blue) edge with each of these sides. These sides only share one edge with each other.
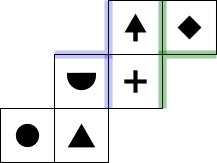
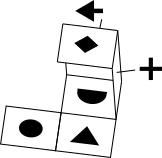
Some of the green and blue edges are shown on the net to the right. It is enough to see that when the face is on the top, the face is at the bottom.
Which Face?
Age 14 to 16
ShortChallenge Level 
Folding up the net
Imagine folding the net into a cube, starting with the face
, and continuing until it reaches the top. So the face
is at the bottom when the face is at the top.Considering edges
Imagine the top and the base of a cube. The top shares a (green) edge with each side that isn't the base. The base shares a (blue) edge with each of these sides. These sides only share one edge with each other.
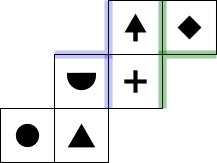
Some of the green and blue edges are shown on the net to the right. It is enough to see that when the face
is on the top, the face is at the bottom.You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Nine Colours
Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?
The Spider and the Fly
A spider is sitting in the middle of one of the smallest walls in a room and a fly is resting beside the window. What is the shortest distance the spider would have to crawl to catch the fly?
Hamiltonian Cube
Weekly Problem 36 - 2007
Find the length along the shortest path passing through certain points on the cube.